Sixteen players S1, S2, S3,…,S16 play in a tournament. Number of ways in which they can be grouped into eight pairs so that S1 and S2 are in different groups, is equal to
715
1415
215
415
The correct Answer is:B
Total ways =16!(2!)88!
Number of ways in which P4 and P9 are in same groups =14!(2!)77!
Number of ways in which they are in different groups
=16!(2!)88!−14!(2!)77!
=14!(2)77!(15.162.(8)−1)=14.14!(2)77!
Probability =14.14!(2)7.7!16!(2)88!=14.8.215.16=1415
Topper's Solved these Questions
Similar Questions
Knowledge Check
SN1 and SN2 reactions are
ABoth stereospecificBBoth stereoselectiveCStereoselective and stereospecific respectivelyDStereospecific and stereoselective respectively
If S0,S1,S2,… are areas bounded by the x-axis and half-wave of the curve y=sinπ√x, then prove that S0,S1,S2,… are in A.P…
View SolutionIdentify number of substrate those can give SN1 and SN2 reaction both.
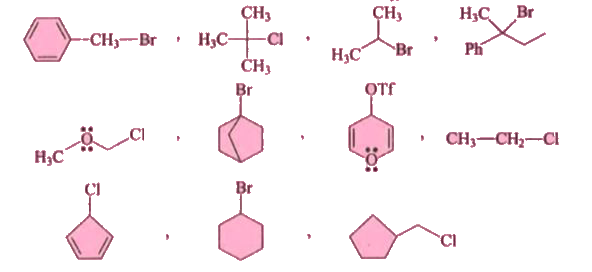
View SolutionThe number of hydroxyl group(s) in N is
_S01_496_Q01.png)
View SolutionIn a knockout tournament 2n equally skilled players, S1,S2,….S2n, are participatingl. In each round, players are divided in pair at random and winner from each pair moves in the next round. If S2 reaches the semi-final, then the probability that S1 wins the tournament is 1/84. The value of n equals _______.
View SolutionLet Sn denote the sum of the first n terms of an A.P.. If S4=16 and S6=−48, then S10 is equal to :
View SolutionIf S1,S2,S3are the sum of first n natural numbers, their squares and their cubes, respectively, show that 9S22=S3(1+8S1).
View SolutionIf S1,S2,S3 are the sums of first n natural numbers, their squares and cubes respectively, show that 9S22=S3(1+8S1).
View Solution

