A circle C1, of radius 2 touches both x-axis and y- axis. Another circle C1 whose radius is greater than 2 touches circle and both the axes. Then the radius of circle is (a) 6−4√2 (b) 6+4√2 (c) 3+2√3 (d) 6+√3
The correct Answer is:2
Let the two circles be as shown in the figure.
The smaller circle is x2+y2=1.
Clearly, from the figure
cos45∘=DEAD
⇒1√2=r−1r+1
⇒r+1=√2r−√2
⇒r=√2+1√2−1=3+2√2
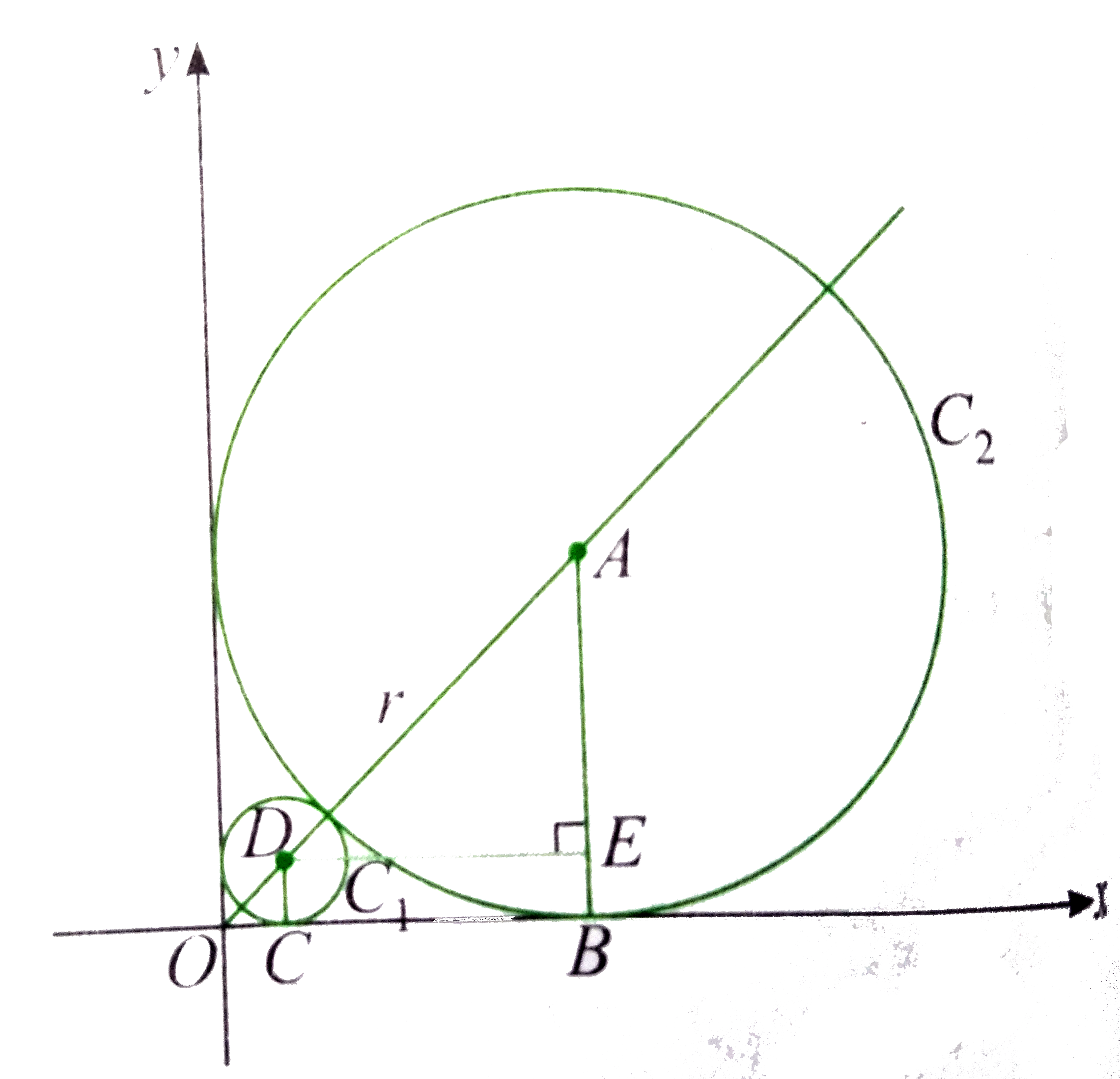
Topper's Solved these Questions
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:Multiple Correct Anser Type
Explore 29 Videos
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:Linked Comprehension Type (For Problem 1-3)
Explore 3 Videos
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:CONCEPT APPLICATION EXERCISE 4.20
Explore 1 Video
- BINOMIAL THEOREMBook:CENGAGE ENGLISHChapter:BINOMIAL THEOREMExercise:Matrix
Explore 4 Videos
- CIRCLESBook:CENGAGE ENGLISHChapter:CIRCLESExercise:Comprehension Type
Explore 8 Videos
Similar Questions
C1 is a circle of radius 1 touching the x- and the y-axis. C2 is another circle of radius greater than 1 and touching the axes as well as the circle C1 . Then the radius of C2 is (a)3−2√2 (b) 3+2√2 3+2√3 (d) none of these
View SolutionThe line 2x−y+1=0 is tangent to the circle at the point (2, 5) and the center of the circle lies on x−2y=4. The radius of the circle is (a) 3√5 (b) 5√3 (c) 2√5 (d) 5√2
View Solution
Knowledge Check
A circle centre (1,2) touches y-axis. Radius of the circle is
A2B3C1D4
If (α,β) is a point on the circle whose center is on the x-axis and which touches the line x+y=0 at (2,−2), then the greatest value of α is (a)4−√2 (b) 6 (c)4+2√2 (d) +√2
View SolutionA circle S of radius 'a' is the director circle of another circle S1,S1 is the director circle of circle S2 and so on. If the sum of the radii of all these circle is 2, then the value of 'a' is (a) 2+√2 (b) 2−1√2 (c) 2−√2 (d) 2+1√2
View SolutionIf C1 (1, 3) and C2(4, 3)are the centres of two circles whose radical axis is y-axis. If the radius of the 1st circle is 2√2 units, then the radius of the second circle is
View SolutionA circle touches the x-axis and also touches the circle with center (0,3) and radius 2. The locus of the center
View SolutionABCD is a square of unit area. A circle is tangent to two sides of ABCD and passes through exactly one of its vertices. The radius of the circle is (a) 2−√2 (b) √2−1 (c) √2−12 (d) 1√2
View SolutionThe radius of the circle passing through the points (1,2),(5,2)and(5,−2) is : (A) 5√2 (B) 2√5 (C) 3√2 (D) 2√2
View SolutionThe radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length, is
View Solution

