A circle touches the x-axis and also touches the circle with center (0,3) and radius 2. The locus of the center
a circle
an ellipse
a parabola
a hyperbola
The correct Answer is:C
(3) Let C1(h,k) be the centre of the circle.
The circle touches the c-axis. Then its radius is r1=k
Also, the circle touches the circle with center C2(0,3) and radius r2=2. Therefore,
|C1C2|=r1+r2
or√(h−0)2+(k−3)2=|k+2|
Squaring, we get
h2−10k+5=0
Therefore, the locus is x2−10y+5=0, which is a parabola.
Topper's Solved these Questions
- PARABOLABOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWER TYPE )
26 Videos
- PARABOLABOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - LINKED COMPREHENSION TYPE
45 Videos
- PARABOLABOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - Concept Applications Exercise 5.7
9 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Numberical Value Type
5 Videos
- PERMUTATION AND COMBINATIONBOOK - CENGAGE ENGLISHCHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Comprehension
8 Videos
Similar Questions
A circle touches the x-axis and also thouches the circle with center (0, 3) and radius 2. The locus of the center of the circle is (a) a circle (b) an ellipse (c) a parabola (d) a hyperbola
View SolutionA circle touches the X-axis and also touches externally the circle with centre (0,3) and radius 2. Show that the locus of the centre of circle is the parabola x2=10y−5.
View Solution
Knowledge Check
A circle centre (1,2) touches y-axis. Radius of the circle is
A2B3C1D4Column AIn the figure, two circle with centers A and B touch a larger circle with center O internally. The ratio of the radii of Circle A to Circle B is 7 : 9Column BOAOB
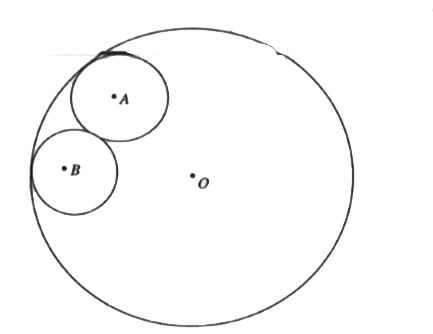 AIf column A is largerBIf column B is largerCIf the columns are equalDIf there is not enough information to decide
AIf column A is largerBIf column B is largerCIf the columns are equalDIf there is not enough information to decide
The circle with centre (4,-1) and touching x-axis is
View SolutionThe circle with centre (2,3) touching x-axis has the radius equal to
View SolutionIf |z|<1,then1+2z lies (A) on or inside circle having center at origin and radius 2 (B) outside the circle having center at origin and radius 2 (C) inside the circle having center at (1,0) and radius 2 (D) outside the circle having center at (1,0) and radius 2.
View SolutionObtain the equation of the circle, radius 2 units, which lies in the positive quadrant and touches both axes of co-ordinates. Find also the equation of the circle, with centre (6, 5) which touches the above circle externally.
View SolutionA circle of radius 2 lies in the first quadrant and touches both the axes. Find the equation of the circle with centre at (6,5) and touching the above circle externally.
View SolutionA circle intersects the X axis at (1,0) and (7,0). If the radius of the circle is 5, what is the sum of the coordinates of the center?
View Solution
