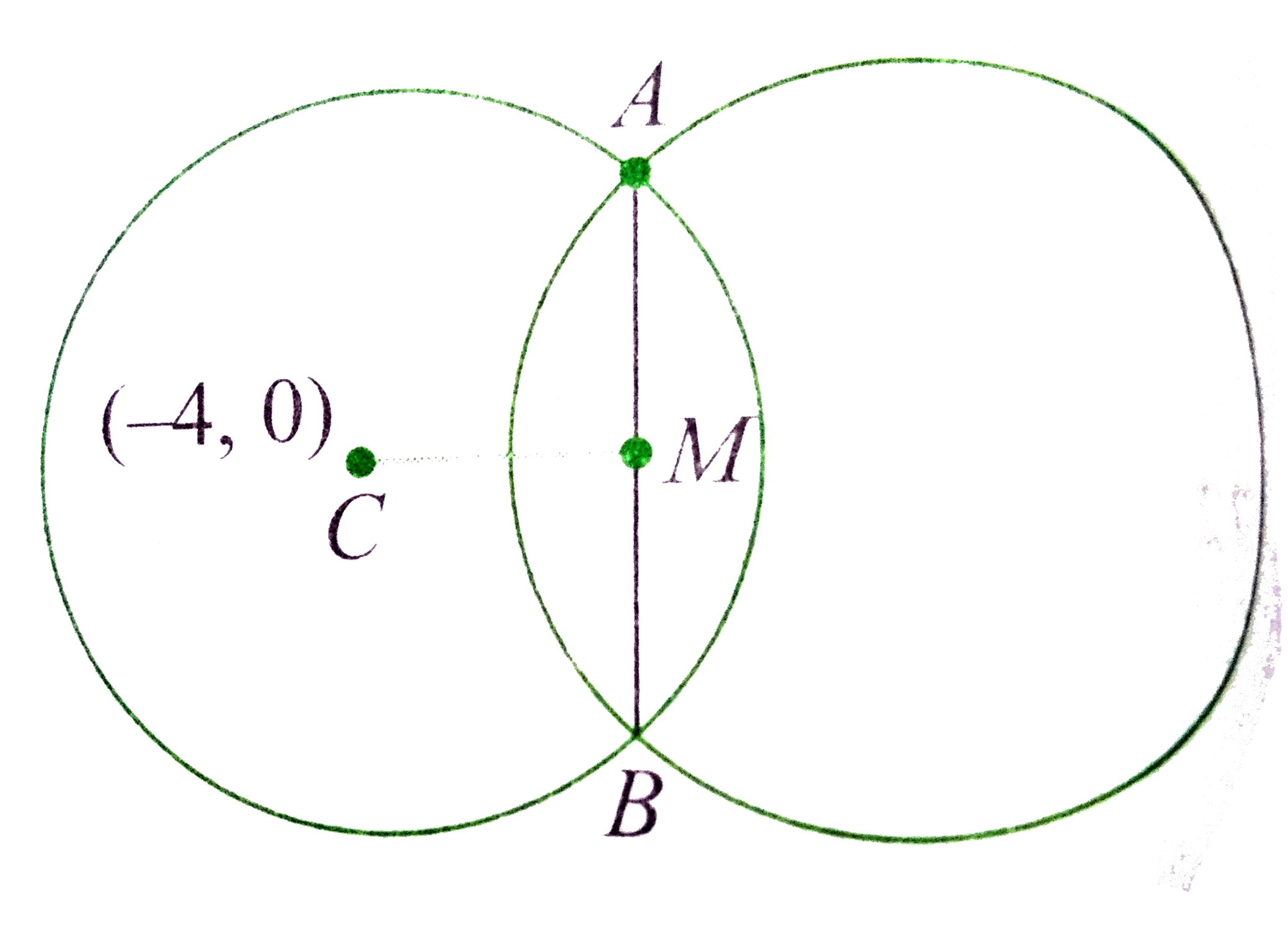
If the length of the common chord of two circles x2+y2+8x+1=0 and x2+y2+2μy−1=0 is 2√6 , then the values of μ are ±2 (b) ±3 (c) ±4 (d) none of these
±2
±3
±4
none of these
The correct Answer is:2
The common choard is S1−S2=0
4x−μy+1=0
∴AC= Radius of first circle =√15
AM=AB2=√6
∴CM=3
∴|−16+1|√16+μ2=3
or μ=±3
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Multiple Correct Anser Type
29 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)
3 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.20
1 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
The length of the common chord of the two circles x2+y2−4y=0 and x2+y2−8x−4y+11=0 is
View SolutionFind the length of the common chord of the circles x2+y2+2x+6y=0 and x2+y2−4x−2y−6=0
View SolutionThe length of the common chord of the circles x2+y2−2x−1=0 and x2+y2+4y−1=0, is
View SolutionThe length of the common chord of the circles x2+y2+ax+by+c=0 and x2+y2+bx+ay+c=0 is
View SolutionThe length of the common chord of the circles (x−6)2+(y−4)2=4,(x−4)2+(y−6)2=4 is
View SolutionCommon chord of the circles x2+y2−4x−6y+9=0,x2+y2−6x−4y+4=0 is
View SolutionFind the length of the common chord of the parabola y2=4(x+3) and the circle x2+y2+4x=0 .
View SolutionFind the length of the common chord of the parabola y2=4(x+3) and the circle x2+y2+4x=0 .
View SolutionThe length of the common chord of the circles (x−a)2+(y−b)2=c2 and (x−b)2+(y−a)2=c2, is
View SolutionIf length of the common chord of the circles x2+y2+2x+3y+1=0andx2+y2+4x+3y+2=0 then the value of [a]. (where [ - ] denotes greatest integer function)
View Solution
