If r1andr2 are the radii of the smallest and the largest circles, respectively, which pass though (5, 6) and touch the circle (x−2)2+y2=4, then r1r2 is (a) 441 (b) 414 541 (d) 416
31/4
41/4
41/3
17
The correct Answer is:2
The given circle is (x−2)2+y2=4, the centre is (2,0), and the radius is 2.
Therefore, distance between (2,0) and (5,6) is √9+36=3√5. Then r1=3√5−22
and r2=d22=3√5+22
∴r1r2=414
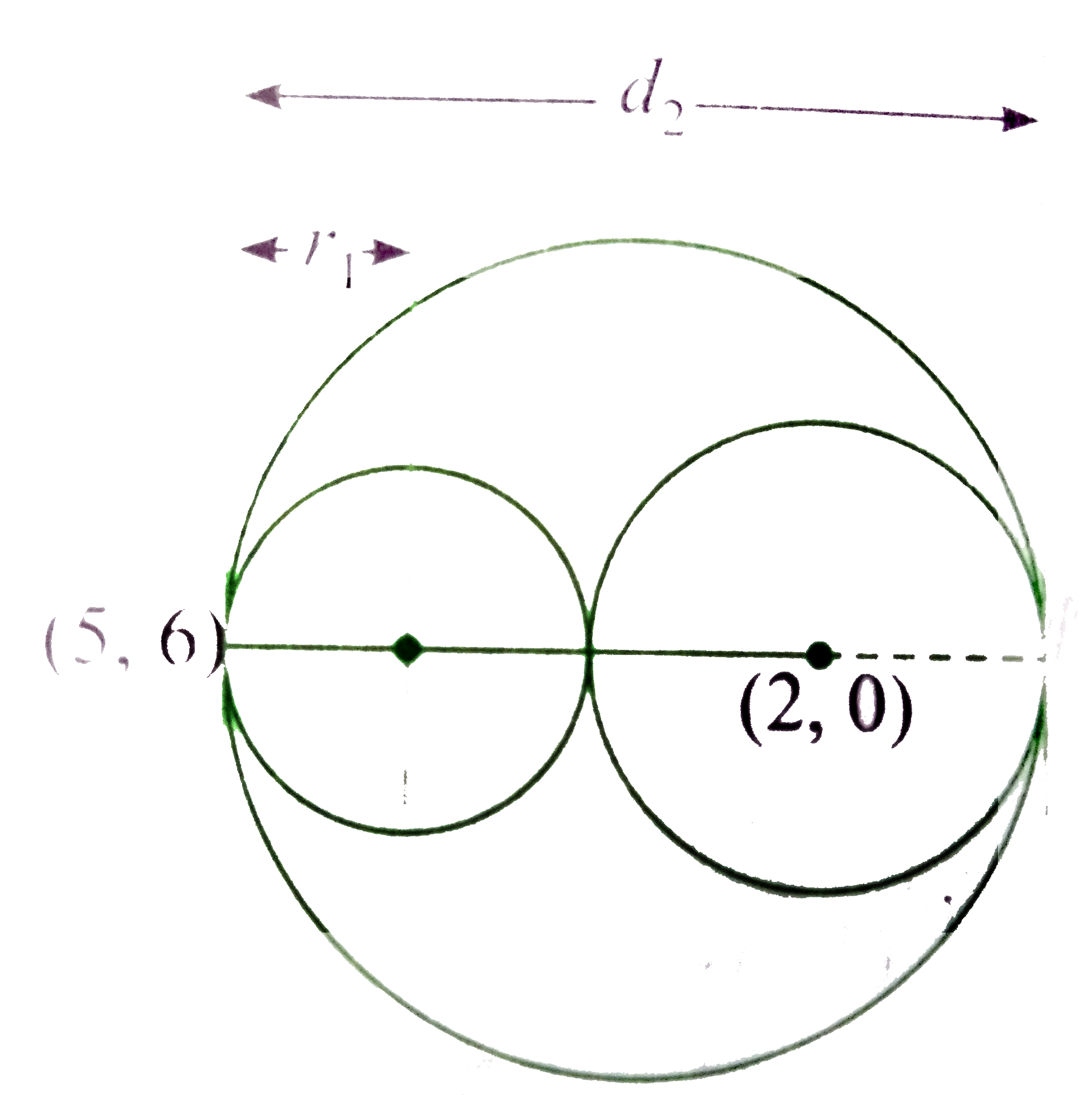
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Multiple Correct Anser Type
29 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)
3 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.20
1 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
If r1andr2 are the radii of the smallest and the largest circles, respectively, which pass though (5, 6) and touch the circle (x−2)2+y2=4, then r1r2 is (a) 441 (b) 414 (c)541 (d) 416
View SolutionIf r1andr2 be the maximum and minimum radius of the circle which pass through the point (4, 3) and touch the circle x2+y2=49, then r1r2 is …….
View SolutionIf r1andr2 be the maximum and minimum radius of the circle which pass through the point (4, 3) and touch the circle x2+y2=49, then r1r2 is …….
View SolutionFind the equation of the circle which passes through (6,5) (4,1) and whose centre lies on 4x+y−16=0
View SolutionIf radii of the smallest and the largest circle passing through (√3,√2) and touching the circle x2+y2−2√2y−2=0 are r1 and r2 respectively, then find the mean of r1 and r2.
View Solutionfind the equation circle which is passes through the points (4,1),(6,5) and centre lies on 4x+y=16 is
View SolutionFind the equation of the circle passing through the points (4,1) and (6,5) and whose centre lies on the line 4x+ y = 16.
View SolutionThe co-ordinates of the middle point of the chord cut off on 2x - 5y +18= 0 by the circle x2+y2−6x+2y−54=0 are (A) (1,1) (B) (2, 4) (C) (4,1) (D) (1, 4)
View SolutionThe orthocentre of the triangle formed by the lines xy=0 and x+y=1 is (a) (12,12) (b) (13,13) (c) (0,0) (d) (14,14)
View SolutionThe equation of a circle is x2+y2=4. Find the center of the smallest circle touching the circle and the line x+y=5√2
View Solution
