Question

The circle which can be drawn to pass through (1, 0) and (3, 0) and to
touch the y-axis intersect at angle $\theta \stackrel{.}{}$
Then $\cos \theta$
is equal to
$\frac{1}{2}$
(b) $-\frac{1}{2}$
(c) $\frac{1}{4}$
(d) $-\frac{1}{4}$

Options

A. `1//2`
B. `1//3`
C. `1//4`
D. `-1//4`

Answer

1

Explanation

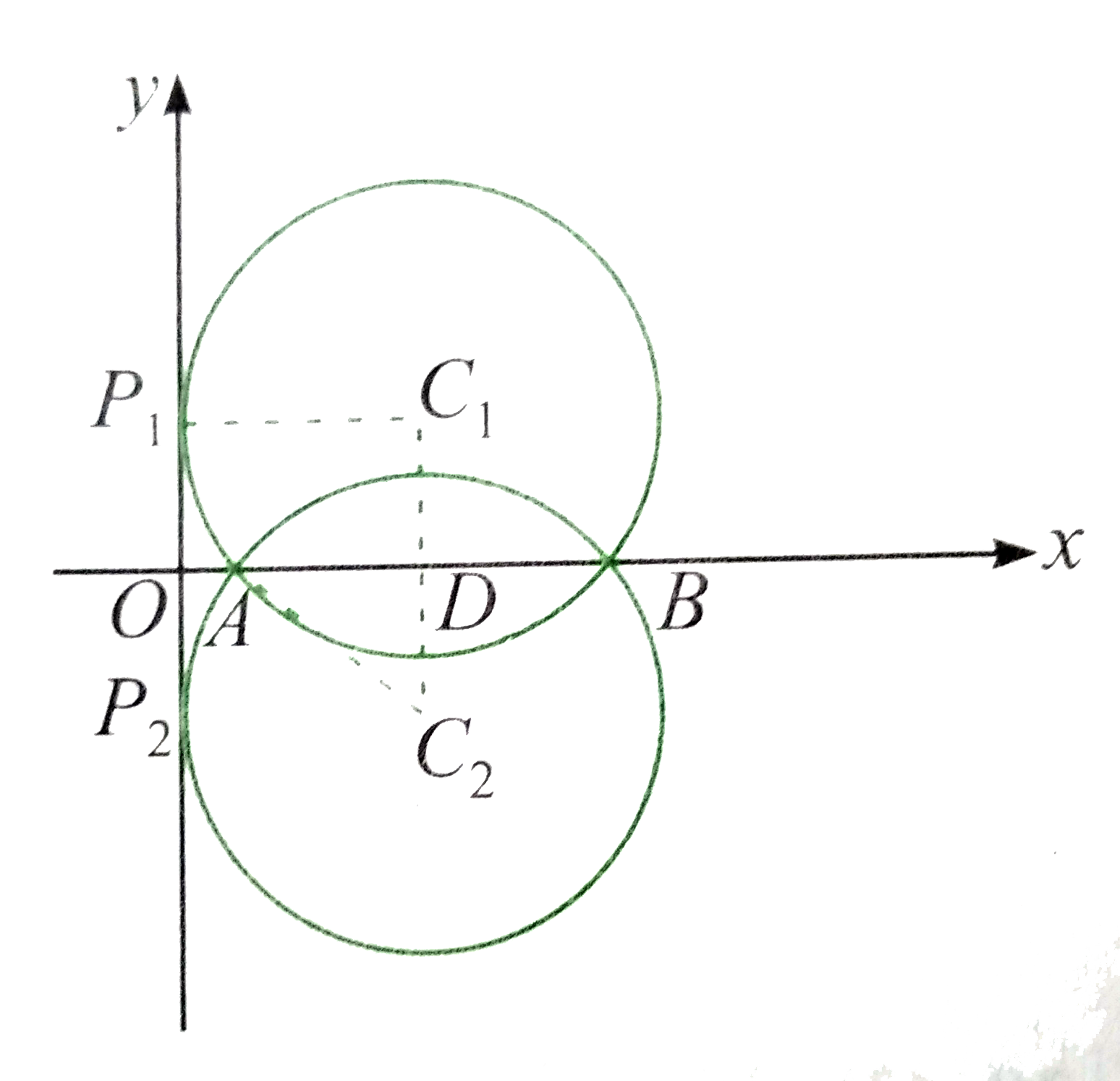
Let `A-=(1,0),B -= (3,0)` and `C_(1)` and `C_(2)` be the centers of circles passing through A and Band touching the y-axis at `P_(1)` and `P_(2)` respectively. If r is the radius ( here radii of both circles will be the same ).
`C_(1)A=C_(2)A=r=OD=2`
and `C_(1)=(2,h)`
or `C_(1) -= (2, sqrt(3)), C_(2)-= (2,-sqrt(3))`
If `/_ C_(1)AC_(2)=theta`, then
`cos theta =(AC_(1)^(2)+AC_(2)^(2)-C_(1)C_(2)^(2))/(2AC_(1)xxAC_(2))=(1)/(2)`