A line meets the coordinate axes at A and B . A circle is circumscribed about the triangle OAB. If d1andd2 are distances of the tangents to the circle at the origin O from the points AandB , respectively, then the diameter of the circle is (a)2d1+d22 (b) d1+2d22 (c)d1+d2 (d) d1d2d1+d2
2d1+d22
d1+2d22
d1+d2
d1d2d1+d2
The correct Answer is:3
Let the circle be x2+y2+2gx+2fy=0.
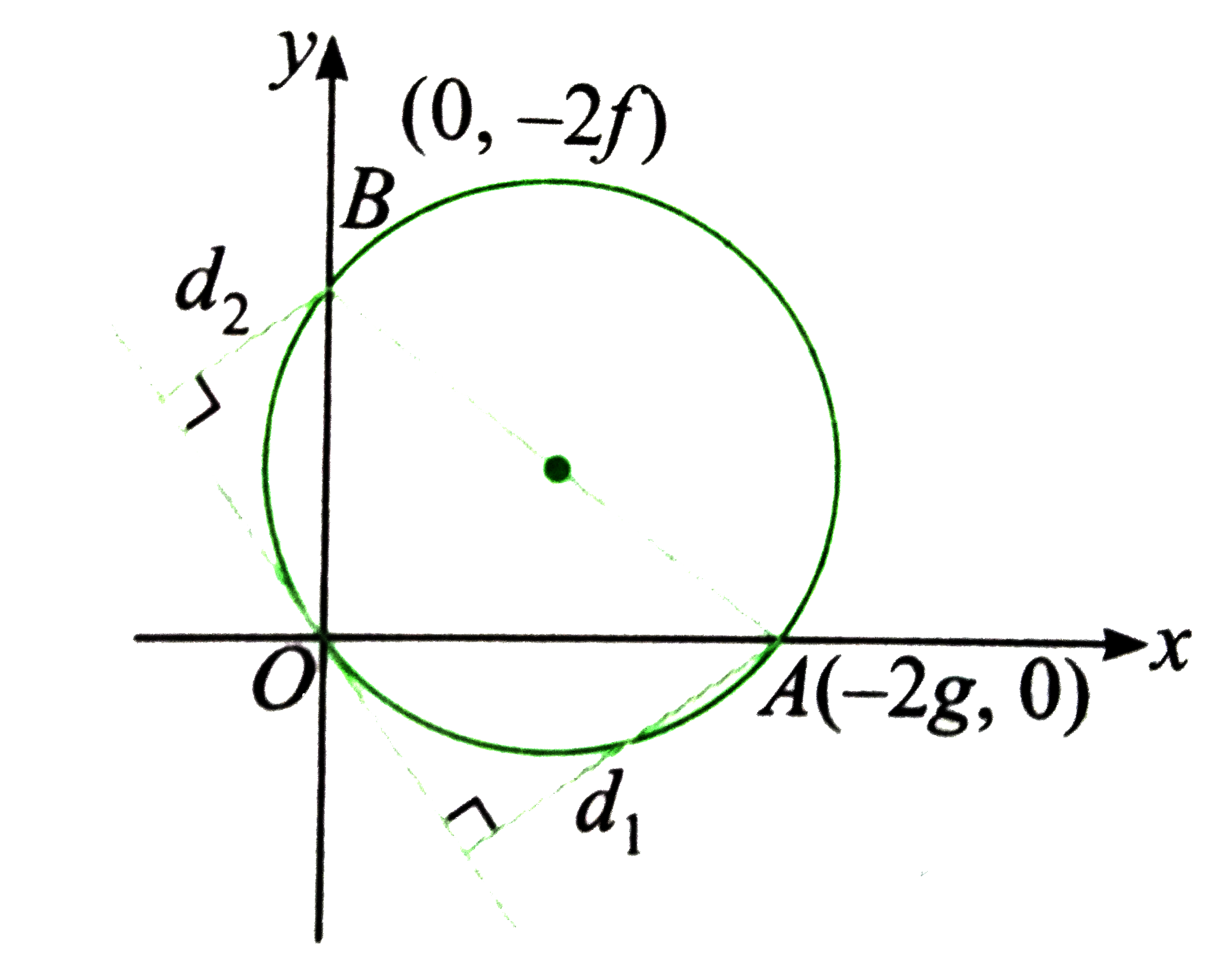
Tangent at the origin is
gx+fy=0
d1=2g2√g2+f2 and d2=2f2√g2+f2
or d1+d2=2√g2+f2
= Diameter of the circle
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Multiple Correct Anser Type
29 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)
3 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.20
1 Video
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
The ratio of the area and circumference of a circle of diameter d is
(a)d
(b) d2
(c)d4
(d) 2 d
View SolutionFind the equation of the circle, the coordinates of the end points of whose diameter are (−1,2)and(4,−3).
View SolutionThe length of the diagonal of a square is d units. The area of the square is (a)d2 (b) 12d2 (c)14d2 (d) 2d2
View SolutionA variable line through the point P(2,1) meets the axes at A an d B . Find the locus of the centroid of triangle OAB (where O is the origin).
View SolutionLet d1andd2 be the length of the perpendiculars drawn from the foci SandS' of the ellipse x2a2+y2b2=1 to the tangent at any point P on the ellipse. Then, SP:S′P= d1:d2 (b) d2:d1 d12:d22 (d) √d1:√d2
View SolutionIf a and b denote the sum of the coefficients in the expansions of (1−3x+10x2)nand (1+x2)n respectively, then write the relation between a and b.
View SolutionABCD is a parallelogram. If the coordinates of A, B, C are (2,3), (1,4)and (0,−2) respectively, find the coordinates of D.
View SolutionIf O is the origin and OPandOQ are the tangents from the origin to the circle x2+y2−6x+4y+8−0 , then the circumcenter of triangle OPQ is (3,−2) (b) (32,−1) (34,−12) (d) (−32,1)
View SolutionABCD is a square of unit area. A circle is tangent to two sides of ABCD and passes through exactly one of its vertices. The radius of the circle is (a) 2−√2 (b) √2−1 (c) √2−12 (d) 1√2
View SolutionAB and CD are diameters of a circle with centre O. If ∠OBD=500, find ∠AOC
View Solution