The locus of the midpoints of the chords of the circle x2+y2−ax−by=0 which subtend a right angle at (a2,b2) is (a)ax+by=0 (b) ax+by=a2+b2 (c) x2+y2−ax−by+a2+b28=0 (d) x2+y2−ax−by−a2+b28=0
ax+by=0
ax+by=a2=b2
x2+y2−ax−by+a2+b28=0
x2+y2−ax−by−a2+b28=0
The correct Answer is:3
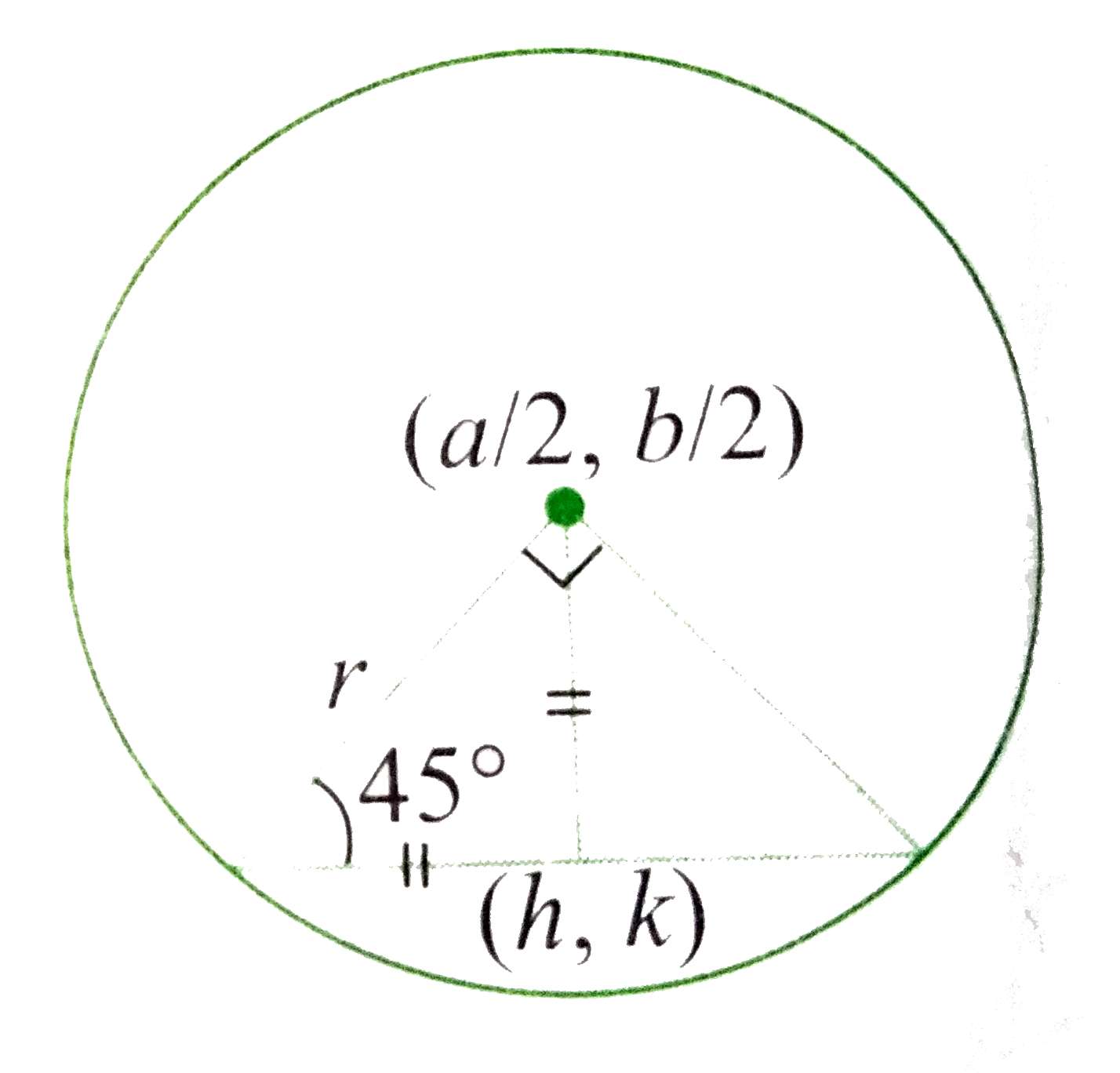
r=√a24+b24=√a2+b22
sin45∘=√(h−a2)2+(h−b2)2√a2+b2/2
or 12=4⎡⎢
⎢⎣(2h−a)24+(2k−b)24a2+b2⎤⎥
⎥⎦
Simplify to get locus x2+y2−ax−by−a2+b28=0
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Multiple Correct Anser Type
29 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)
3 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.20
1 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Find the locus of the midpoint of the chords of the circle x2+y2−ax−by=0 which subtend a right angle at the point (a2,b2). is
View SolutionThe locus of the midpoint of a chord of the circle x2+y2=4 which subtends a right angle at the origins is (a) x+y=2 (b) x2+y2=1 x2+y2=2 (d) x+y=1
View SolutionThe locus of the midpoint of a chord of the circle x2+y2=4 which subtends a right angle at the origins is (a) x+y=2 (b) x2+y2=1 (c)x2+y2=2 (d) x+y=1
View Solutionx+y=a+b,ax−by=a2−b2
View Solutionxa−yb=0, ax+by=a2+b2
View SolutionThe locus of the mid-point of a chord of the circle x2+y2−2x−2y−23=0, of length 8 units is : (A)x2+y2−x−y+1=0 (B) x2+y2−2x−2y−7=0 (C) x2+y2−2x−2y+1=0 (D) x2+y2+2x+2y+5=0
View SolutionEquation of the diameter of the circle x2+y2−2x+4y=0 which passes through the origin is a.x+2y=0 b.x-2y=0 c. 2x+y=0d.2x-y=0.
View SolutionComprehension (Q. 5 & 6) Let AB be any chord of the circle x2+y2−2x−6y−6=0 which subtends a right angle at the point (2, 4). Locus of mid point of AB is x2+y2−7y−16=0 x2+y2−3x−7y+7=0 x2+y2+3x+7y−16=0 x2+y2+3x+7y−7=0
View SolutionSolve: x+y=a+b ; ax−by=a2−b2
View SolutionAB is any chord of the circle x2+y2−6x−8y−11=0 which subtends an angle π2 at (1,2). If locus of midpoint of AB is a circle x2+y2−2ax−2by−c=0; then find the value of (a+b+c).
View Solution
