find the equation of the tangent to the curve y=−5x2+6x+7 at the point (1/2,35/4)
The correct Answer is:A, D
For α=1
y=|x−1|+|x−2|+x=⎧⎪⎨⎪⎩3−xx<11+x1≤x<23x−3x≥2
For α=0,y=3
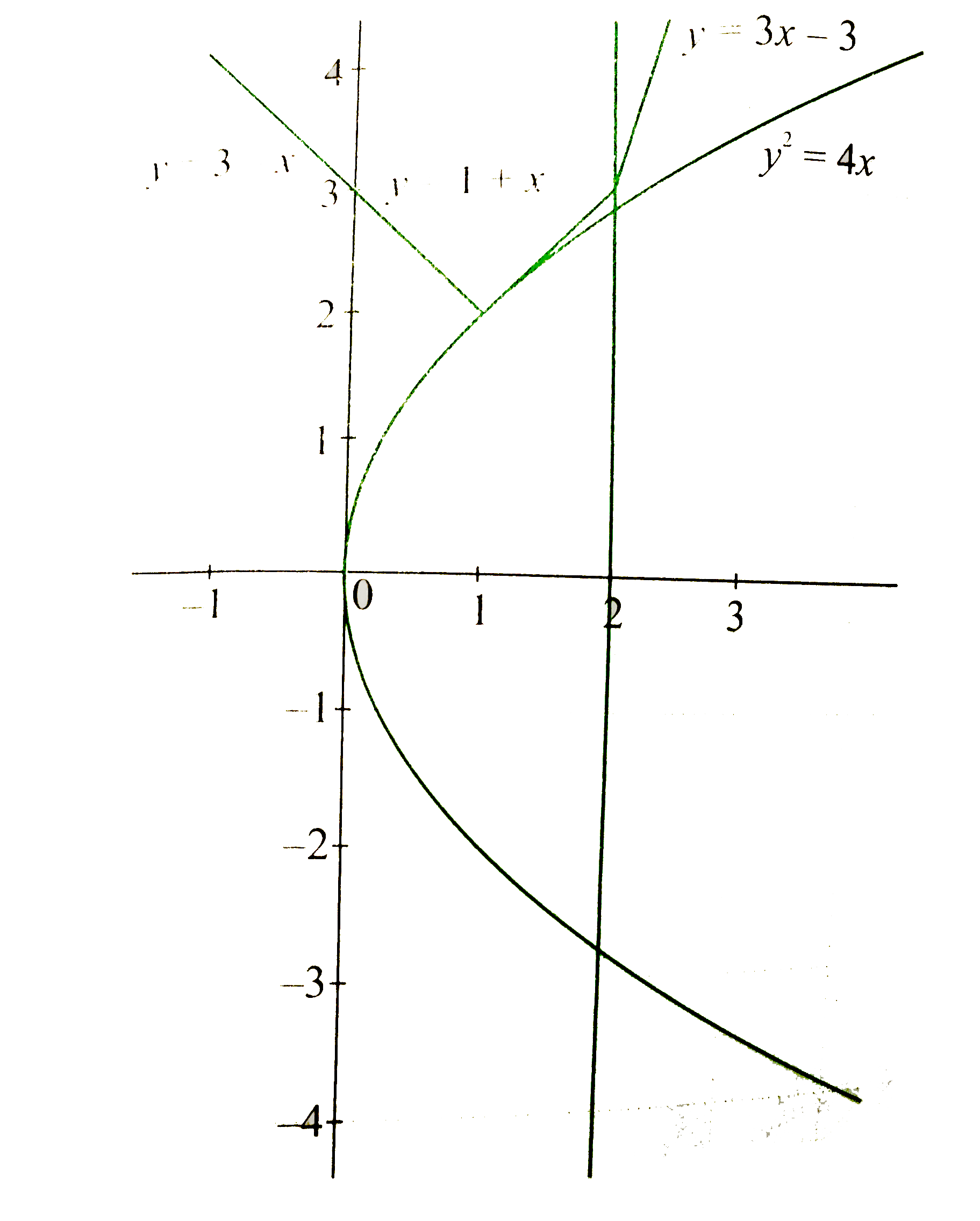
A=12(2+3)×1+12(2+3)×1−2∫02√xdx
⇒ A=5−83√2
∴ F(1)+83√2=5
For α=0,y=|−1|+|−2|=3
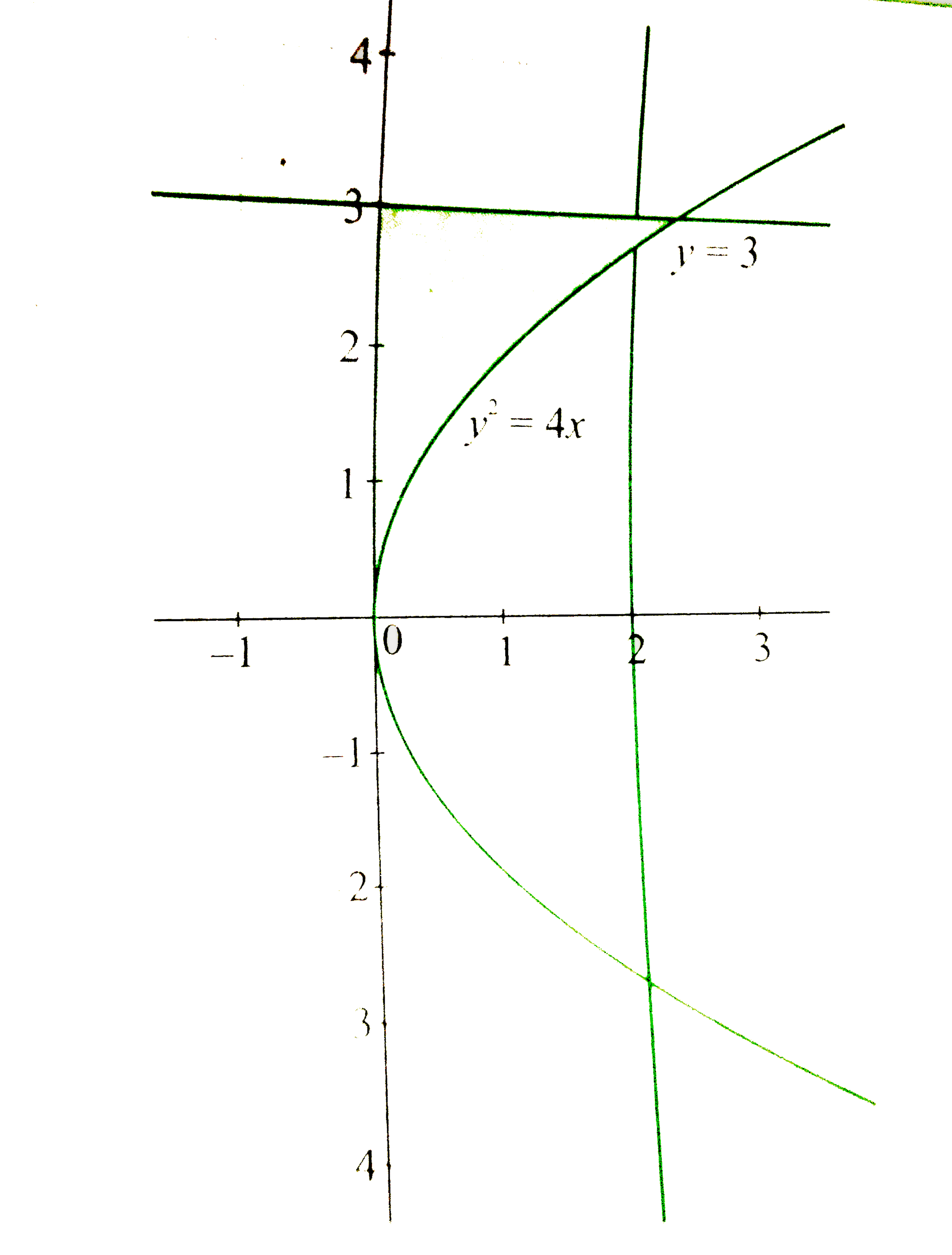
A=6−2∫02√xdx
⇒ A=6−83√2
∴ F(0)+83√2=6
Note : Solutions of the remaining parts are given in their respective chapters.
Topper's Solved these Questions
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Numerical Value Type
18 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Archives
10 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Linkded Comprehension Type
21 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
Similar Questions
Find the equation of the tangent to the curve y=x−sinxcosx at x=π2
View SolutionFind the equation of tangent of the curve x=at2,y=2at at point 't'.
View SolutionFind the equation of tangent to curve y=3x2+4x+5 at (0,5).
View SolutionFind the equation of tangent of the curve 6y=9−3x2 at point (1,1).
View SolutionFind the equation of the tangent to the curve y=x−7(x−2)(x−3) at the point where it cuts the x-axis.
View SolutionFind the equations of the tangent to the curve y2=x34−x at point (2, −2) on it
View SolutionFind the equation of the tangent to the curve √x+√y=a, at the point (a24,a24).
View SolutionFind the equation of the tangent to the curve y=(x3−1)(x−2) at the points where the curve cuts the x-axis.
View SolutionFind the equation of the tangent to the curve y=(x3−1)(x−2) at the points where the curve cuts the x-axis.
View SolutionFind the length of the tangent for the curve y=x3+3x2+4x−1 at point x=0.
View Solution
