show that the tangents to thre curve at the point where x=2 and x=-2 are parallel
The correct Answer is:A, B, C, D
a. sq. units.

b. both the curve are symmetric about y-axis

sq. units.
c.
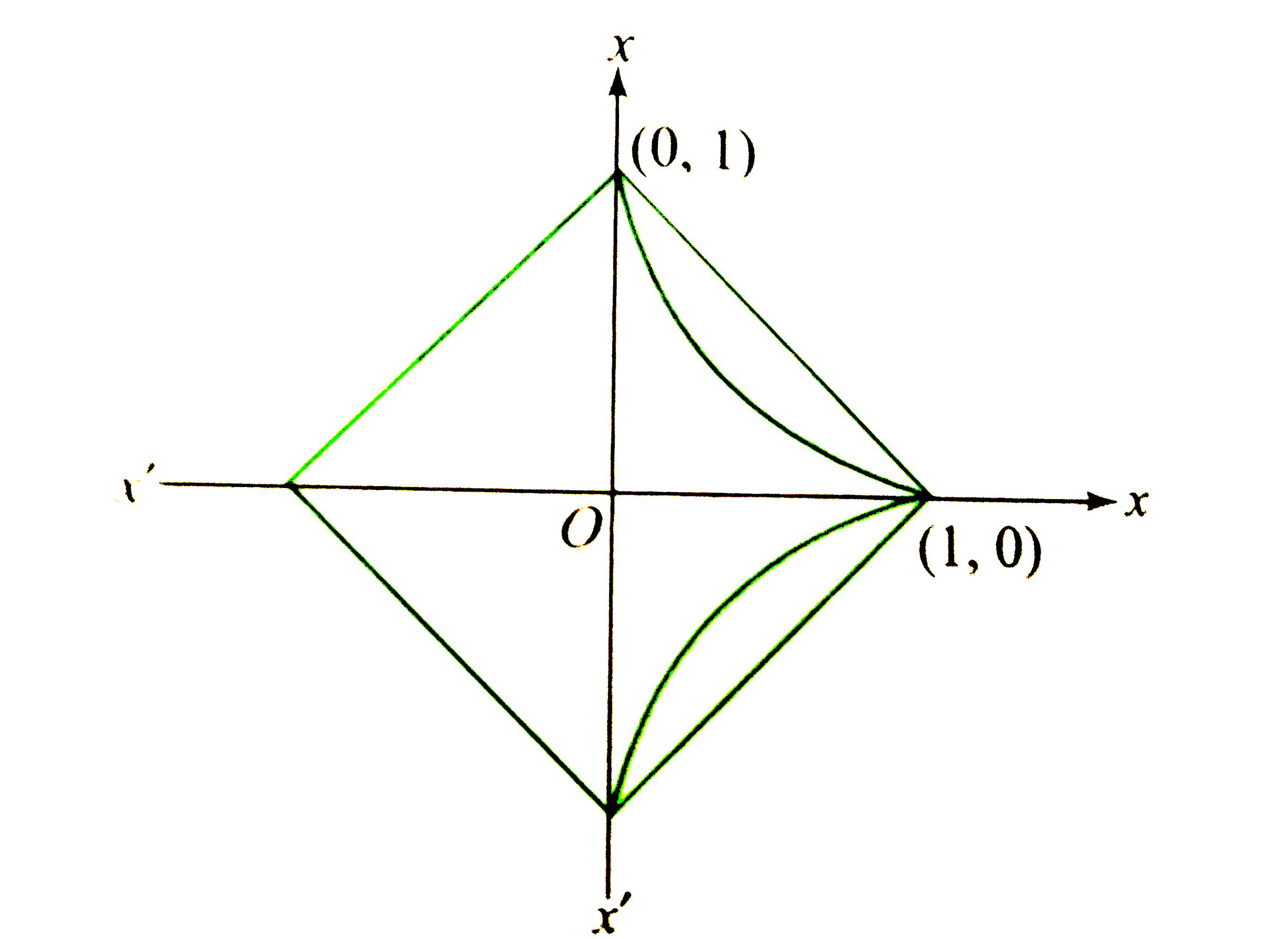
The curve is symmetrical about x-axis
sq. units.
d. If then y=2.
and so on
Intersection of
Intersection of .
.
other integral, except in the interval
Required area (shaded region )
=4 sq. units.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Numerical Value Type18videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Archives10videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Linkded Comprehension Type21videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type5videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix4videos
BINOMIAL THEOREM
Similar Questions
Show that the tangents to the curve y=2x3−3 at the points where x=2 and x=−2 are parallel.
View SolutionShow that the tangents to the curve y=x3−3 at the points where x=2and x=−2 are parallel.
View SolutionShow that the tangents to the curve y=7x3+11 at the points where x=2 and x=−2 are parallel.
View SolutionShow that the tangents to the curve y=7x3+11 at the points x=2 and x=−2 are parallel.
View SolutionProve that the tangents to the curve y=x2−5x+6 at the points (2, 0) and (3, 0) are at right angles.
View SolutionThe slope of the tangent to the curve y=x2−x at the point where the line y = 2 cuts the curve in the first quadrant, is
View SolutionFind the equation of the tangent to the curve y=(x3−1)(x−2) at the points where the curve cuts the x-axis.
View SolutionFind the equation of the tangent to the curve y=(x3−1)(x−2) at the points where the curve cuts the x-axis.
View SolutionWrite the equation of the tangent to the curve y=x2−x+2 at the point where it crosses the y-axis.
View SolutionFind the equation of the tangent to the curve y=x−7(x−2)(x−3) at the point where it cuts the x-axis.
View Solution
