The area of the region bounded by the parabola (y−2)2=x−1, the tangent to the parabola at the point (2,3) and the X-axis is
3
6
9
12
The correct Answer is:C
The given parabola is (y−2)2=x−1. So
dydx=12(y−2)
At(2,3),
dydx=12(3−2)=12
Tangent at (2,3) is
y−3=12(x−2)⇒x−2y+4=0
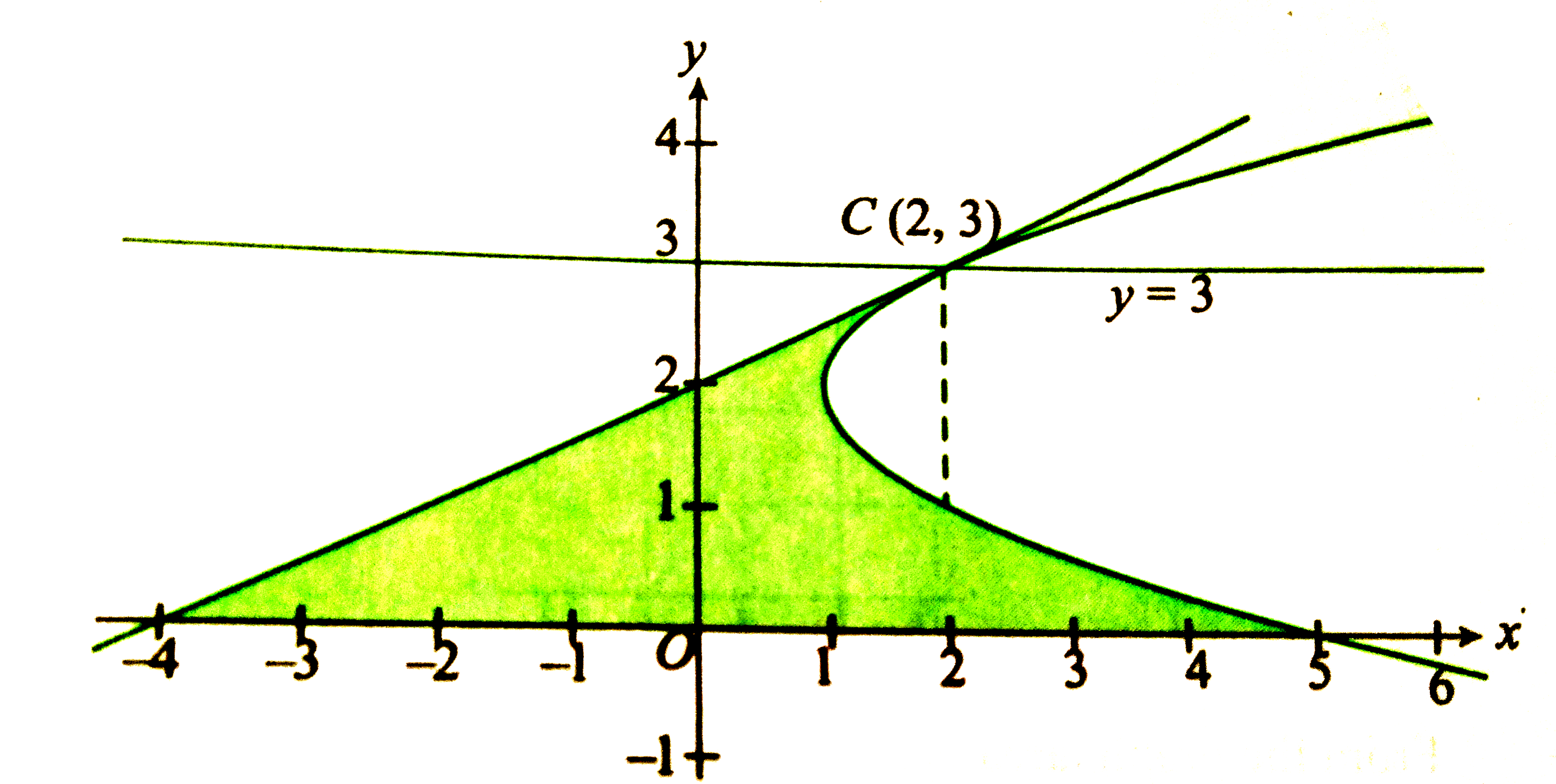
Therefore, the required area
=3∫0[(y−2)2+1]dy−3∫0(2y−4)dy
=∣∣
∣∣(y−2)33+y∣∣
∣∣30−∣∣y2−4y∣∣30
=13+3+83−(9−12)
=9 sq. units
Topper's Solved these Questions
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Single Correct Answer Type
30 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Multiple Correct Answer Type
3 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Numerical Value Type
18 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
Similar Questions
The area of the figure bounded by the parabola (y−2)2=x−1, the tangent to it at the point with the ordinate y=3, and the x-axis is
View SolutionIf Δ be the area in square units of the region bounded by the parabola y=−x2−2x+3, the line tangent to it at the point P(2,−5) and the y-axis, then 3Δ is equal to…
View SolutionFind the area of the region bounded by the parabola y=x2 and y=|x| .
View SolutionFind the area of the region bounded by the parabola y=x2 and y=|x|.
View SolutionThe area of the region bounded by the parabolas x=−2y2 and x=1−3y2 is
View SolutionThe mirror image of the parabola y2=4x in the tangent to the parabola at the point (1, 2) is:
View SolutionThe area (in sq. units) bounded by the parabola y=x2−1, the tangent at the point (2,3) to it and the y-axis is
View SolutionThe area of the region bounded by parabola y2=x and the straight line 2y=x is
View SolutionFind the area of the region bounded by the parabola y2=2pxandx2=2py.
View SolutionFind the area of the region bounded by: the parabola y=x2 and the line y=x
View Solution
