The area of the region enclosed by the curve y=x,x=e,y=1x and the positive X-axis is
52 square units
12 square units
1 square units
32 square units
The correct Answer is:D
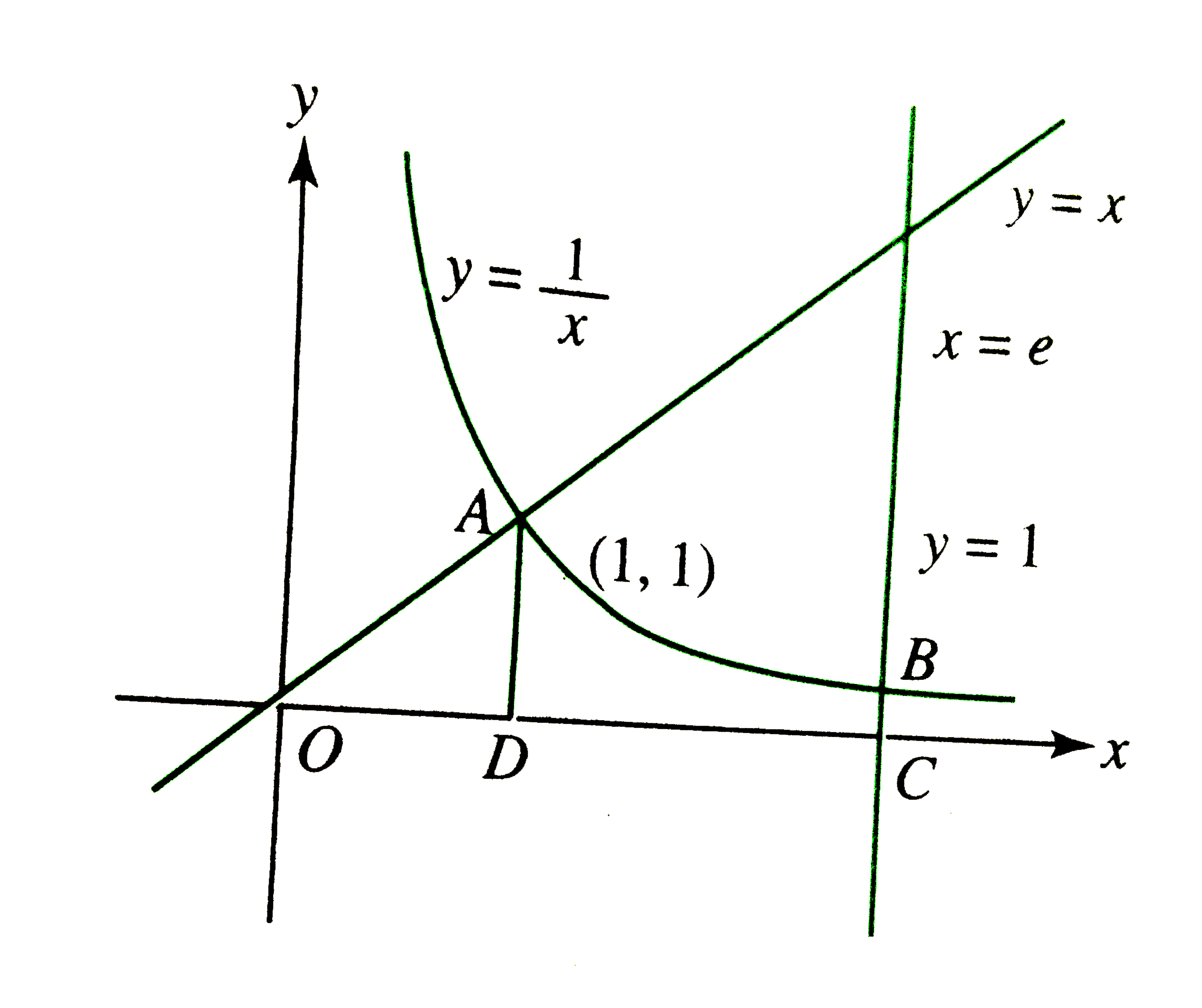
Required area = Area of ΔAOB + Area of region ADCB
=12×1×1+e∫11xdx
=12+[In x]e1
=12+1−0=32 sq. units
Topper's Solved these Questions
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Single Correct Answer Type
30 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Multiple Correct Answer Type
3 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Numerical Value Type
18 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
Similar Questions
The area of the region enclosed by the curves y=x,x=e,y=1x and the positive x-axis is
View SolutionThe area of the region enclosed by the curves y=x,x=e,y=1x and the positive x-axis is (1) 12 square units (2) 1 square units (3) 32 square units (4) 52 square units
View SolutionThe area of the region enclosed by the curve |y|=−(1−|x|)2+5, is
View SolutionThe area of the region bounded by the curves y=|x−2|,x=1,x=3 and the x-axis is
View SolutionFind the area of the region enclosed by the curves
y=x2 and y = 2x
View SolutionFind the area of the region enclosed by the curves
y=x2−4x+3 and the x-axis
View SolutionThe area of the region bounded by the curves y=xex,y=ex and the lines x=±1, is equal to
View SolutionFind the area of the region enclosed by the curves y=x2 and y=x3
View SolutionFind the area of the region enclosed by the curves y=xlogx and y=2x−2x2.
View SolutionThe area of the region bounded by the curve y=sin2x, y-axis and y=1 is :
View Solution
