The area (in sq. units) of the region described by {x,y):y2≤2xandy≥4x−1} is
732
564
1564
932
The correct Answer is:D
y2≤2x represents the interior of parabola y2=2x (towards focus) and y≥4x−1 represents the half region of plane to the left of the line y=4x−1.
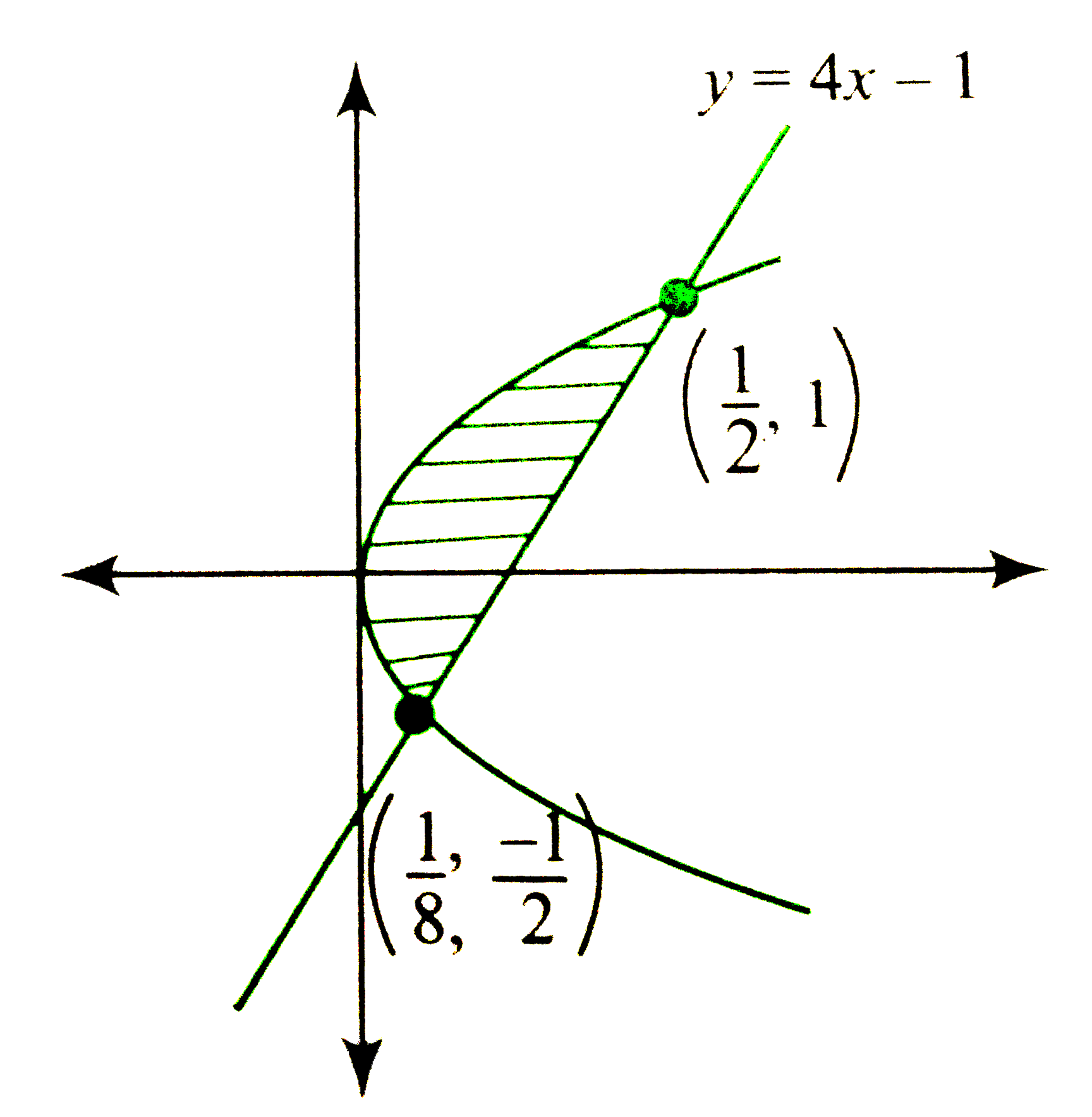
1∫−1/2(y+14−y22)dy=14{y22+y}1−1/2−16{y3}1−1/2
=14{(12+1)−(18−12)}−16{1+18}
=14{32+38}−16{98}=1532−632=932
Topper's Solved these Questions
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Single Correct Answer Type
30 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Multiple Correct Answer Type
3 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Numerical Value Type
18 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
Similar Questions
The area (in square units) of the region bounded by y2=2xandy=4x−1 , is
View SolutionThe area (in sq. units) of the region
{(x,y):y2≤2xandx2+y2≤4x,x≥0,y≤0},is
View SolutionThe area (in sq. units) of the region
{(x,y):y2≤2xandx2+y2≤4x,x≥0,y≤0},is
View SolutionThe area (in sq units) of the region
A={(x,y):y22≤x≤y+4} is
View SolutionThe area (in sq units) of the region A={(x,y):x2≤y≤x+2} is
View SolutionThe area (in sq units) of the region A={(x,y):x2≤y≤x+2} is
View SolutionThe area (in sq. units) of the region bounded by the curves y=2−x2andy=|x| is k, then the value of 3k is
View SolutionThe area (in sq. units) of the region bounded by the curves y=2x and y=|x+1|, in the first quadrant is :
View SolutionThe area (in sq. units) of the region bounded by the parabola y=x2+2 and the lines y=x+1,x=0 and x=3, is
View SolutionThe area (in sq units) of the region {(x,y):y2≥2xandx2+y2≤4x,x≥0,y≥0} is
View Solution
