Find the point on the curve $y = x^{3} - 11 x + 5$ at which the tangent has the equation $y = x - 11$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

a.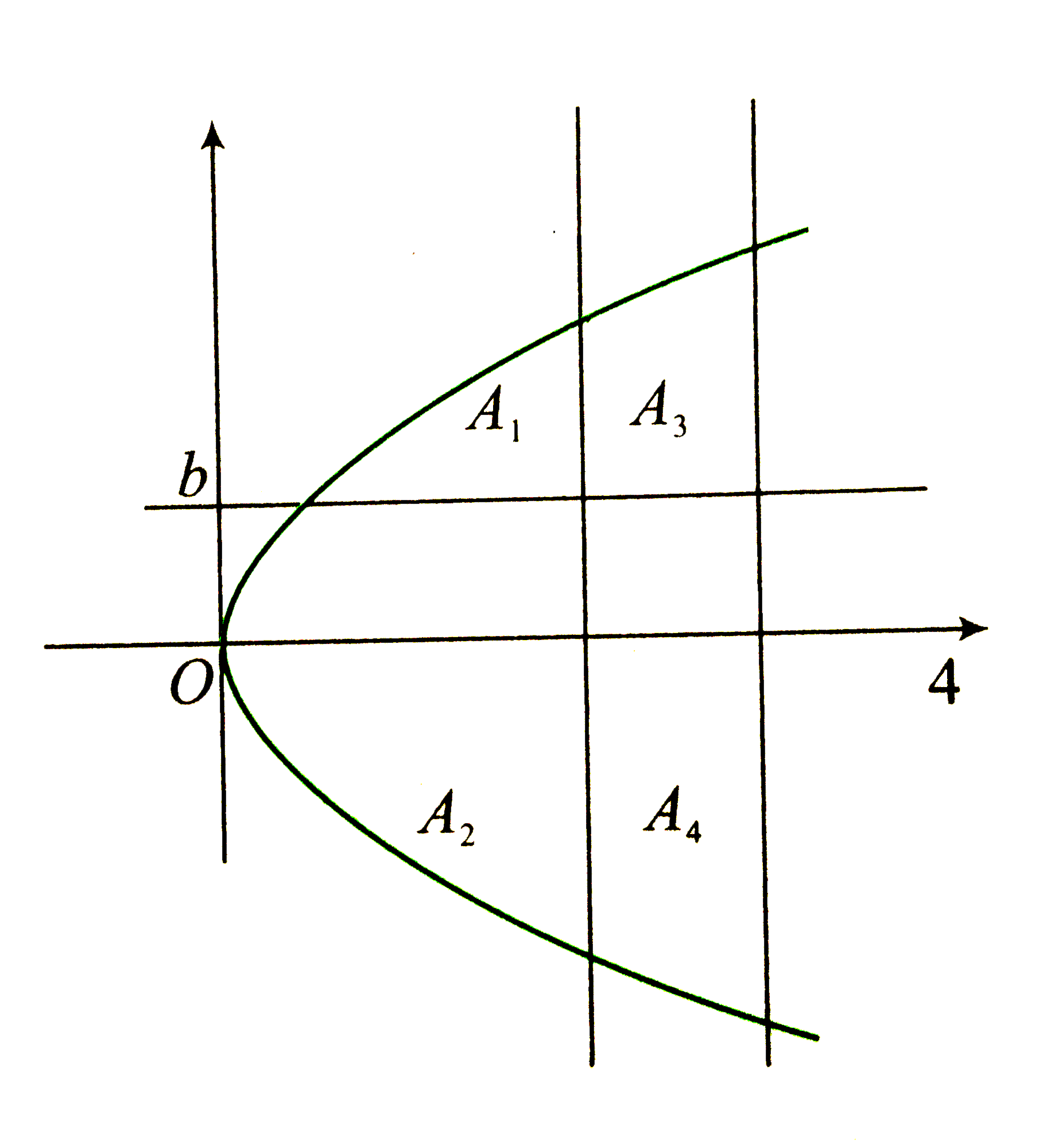
$Total area = 2 4 \int 0 \sqrt{x} d x = \frac{32}{3}$
$Area of each part = 8 / 3$
$A_{3} = A_{4} \Rightarrow 4 \int a (\sqrt{x} - b) d x = 4 \int a (b + \sqrt{x}) d x = \frac{8}{3}$
$∴ b = 0$
$∴ 4 \int a \sqrt{x} d x = \frac{8}{3}$
$∴ a^{3} = 16$
b. $f (x) = {\begin{matrix} x^{\frac{1}{{log}_{e} x}}, & x \neq 1 e, & x = 1 \end{matrix} = {\begin{matrix} x^{\frac{1}{{log}_{e} x}}, & x \neq 1 e, & x = 1 \end{matrix} = e$
Hence required area bound by $y = f (x) and y = | x - e | is e^{2}$
c.

Area = Area of rectangle $O A B C - e In 1 x d x$
$= e - 1$ sq. units.
d. Solving $2 cos x = 3 tan x w e \geq t, 2 - 2 {sin}^{2} x = 3 sin x$
$\Rightarrow sin x = \frac{1}{2} \Rightarrow x = \frac{π}{6}$
$Required area = π / 6 \int 0 (2 cos x - 3 tan x) d x$
$= {(2 sin x - 3 In sec x)}_{0}^{π / 6}$
$= 1 + \frac{3}{2} {log}_{e} 3 - 3 {log}_{e} 2$

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-AREA-Matrix Match Type

Home
Ask Doubt
Profile