If S is the sum of cubes of possible value of c for which the area of the figure bounded by the curve y=8x2−x5, then straight lines x=1andx=c and the abscissa axis is equal to 163, then the value of [S],where[.] denotest the greatest integer function, is____
The correct Answer is:2
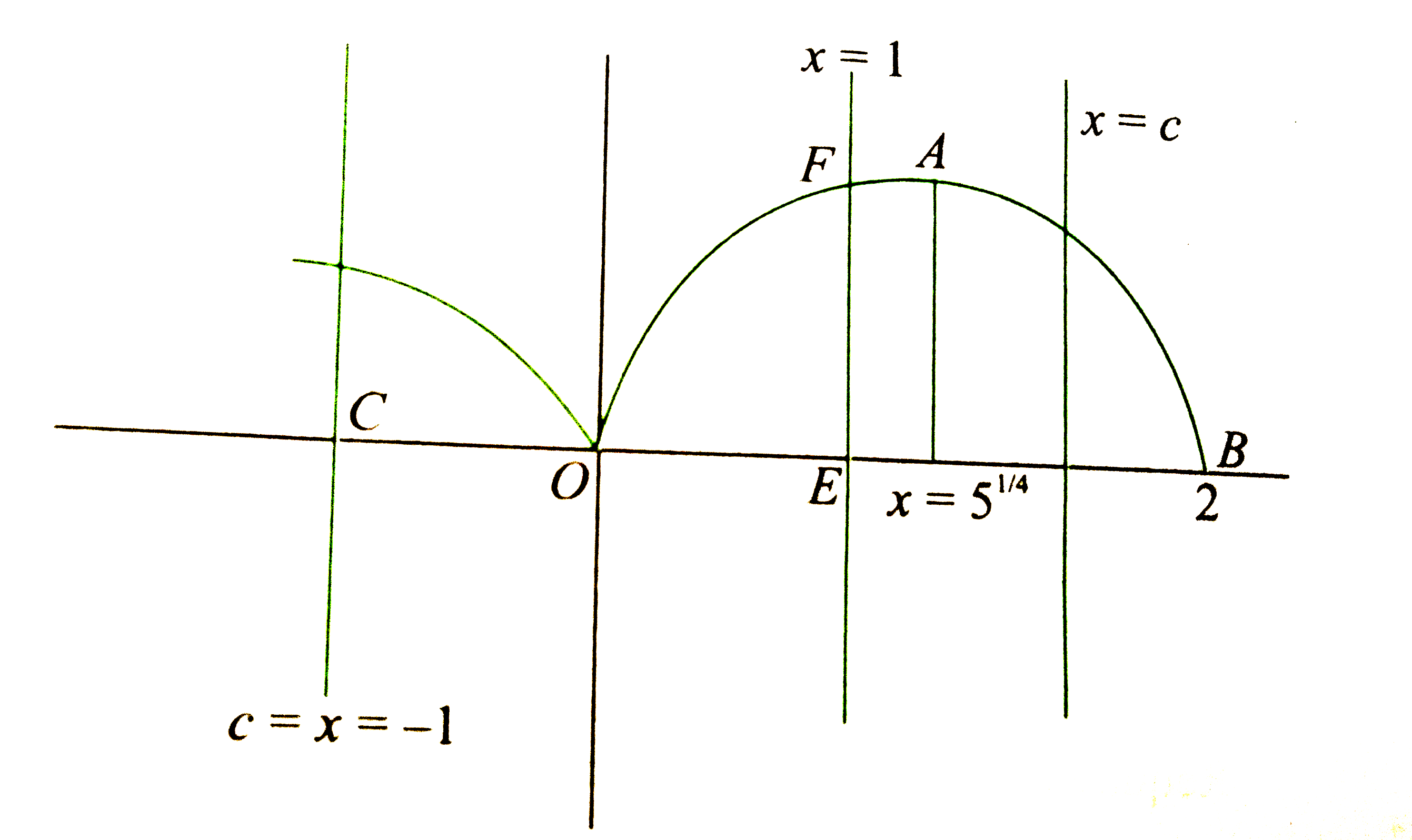
Given that c∫1ydx=163
⇒ c∫1(8x2−x5)dx=163c=(8−√17)1/3 (c>0)
Area OFE=c∫0(8x2−x5)dx=83 (C>0)
so c=−1
Hence, c=−1and(8−√17)1/3
Topper's Solved these Questions
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Archives
10 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Single Correct Answer Type
30 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Matrix Match Type
5 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
Similar Questions
Which of the following abnormalities is due to X-linked recessive mutation ?
View SolutionWhich of the following is the possible value/values of c for which the area of the figure bounded by the curves y=sin2x, the straight lines x=π/6,x=c and the abscissa axis is equal to 1/2?
View SolutionEvaluate:- ∫π0[cotx]dx,where[.] denotes the greatest integer function.
View SolutionEvaluate: ∫20[x2−x+1]dx,where[.] denotos the greatest integer function.
View SolutionEvaluate: ∫20[x2−x+1]dx,where[.] denotos the greatest integer function.
View SolutionEvaluate: ∫5−5x2[x+12]dx(where[.] denotes the greatest integer function).
View SolutionEvaluate: ∫e61[logx3]dx,where[.] denotes the greatest integer function.
View SolutionFind the value of : ∫100e2x−[2x]d(x−[x])where[.] denotes the greatest integer function).
View SolutionFind the value of : ∫100e2x−[2x]d(x−[x])where[.] denotes the greatest integer function).
View SolutionThe area of the region bounded by the curves y=xex,y=ex and the lines x=±1, is equal to
View Solution
