Let C be a curve passing through M(2,2) such that the slope of the tangent at any point to the curve is reciprocal of the ordinate of the point. If the area bounded by curve C and line x=2 is A, then the value of 3A2 is__.
The correct Answer is:8
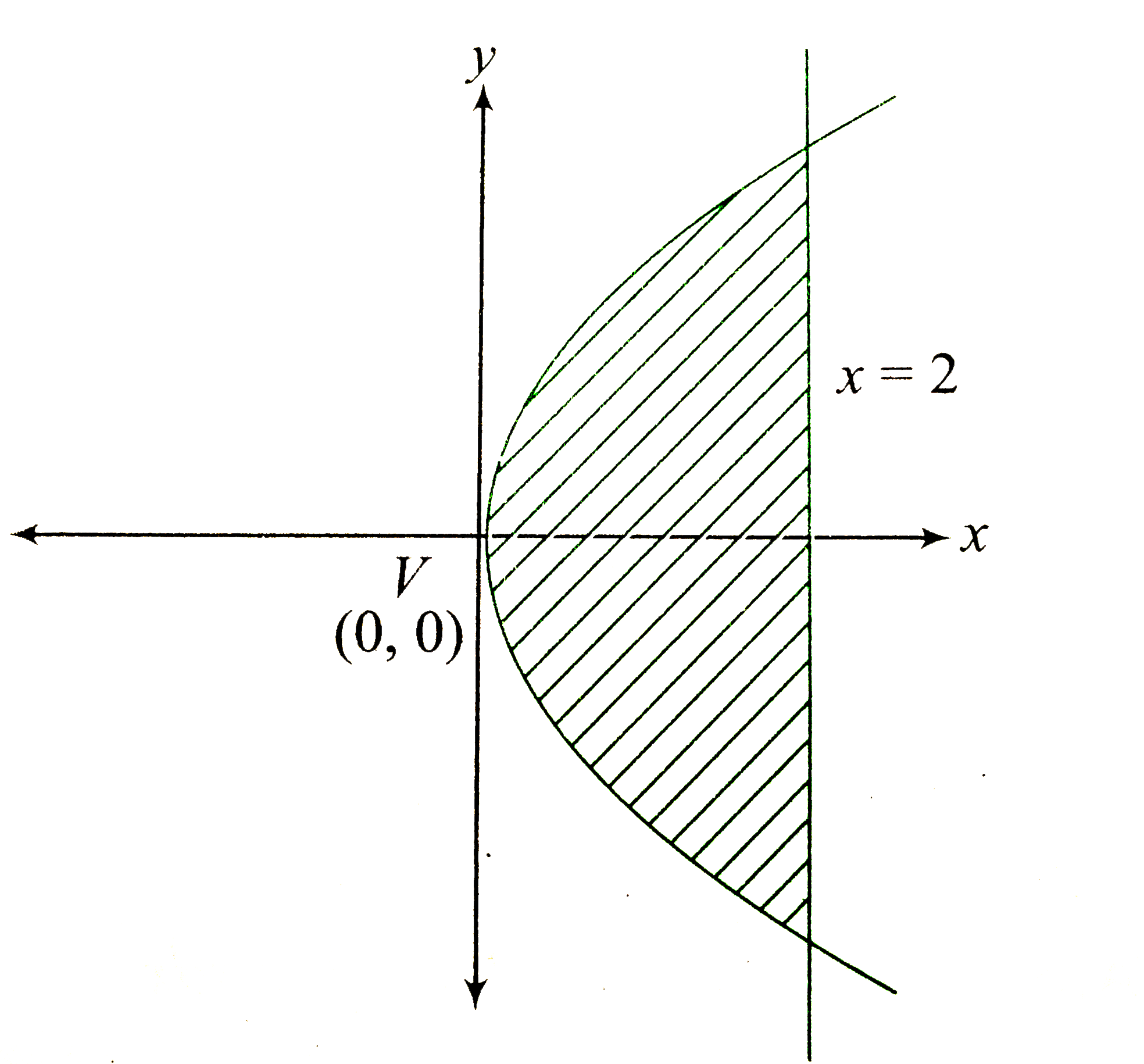
Let P(x,y) be any point on the curve C.
Now, dydx=1y
or ydy=dx⇒y22=x+k
Since the curve passes through M(2,2), so k=0
⇒ y2=2x
∴ Required area =22∫0√2xdx=2√2×23(x3/2)20
=43√2×2√2=163 sq. unit
Topper's Solved these Questions
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Archives
10 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Single Correct Answer Type
30 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Matrix Match Type
5 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
Similar Questions
The curve for which the slope of the tangent at any point is equal to the ration of the abcissa to the ordinate of the point is
View SolutionThe slope of a curve, passing through (3,4) at any point is the reciprocal of twice the ordinate of that point. Show that it is parabola.
View SolutionThe slope of the tangent to the curve at any point is reciprocal of twice the ordinate of that point. The curve passes through the point (4,3). Determine its equation.
View SolutionThe slope of the tangent to the curve at any point is reciprocal of twice the ordinate of that point. The curve passes through the point (4,3). Determine its equation.
View SolutionFind the equation of a curve passing through the origin given that the slope of the tangent to the curve at any point (x, y) is equal to the sum of the coordinates of the point.
View SolutionFind the equation of a curve passing through the origin given that the slope of the tangent to the curve at any point (x, y) is equal to the sum of the coordinates of the point.
View SolutionThe x-intercept of the tangent to a curve is equal to the ordinate of the point of contact. The equation of the curve through the point (1,1) is
View SolutionA curve y=f(x) passes through point P(1,1) . The normal to the curve at P is a (y−1)+(x−1)=0 . If the slope of the tangent at any point on the curve is proportional to the ordinate of the point, then the equation of the curve is
View SolutionA curve y=f(x) passes through the point P(1,1). The normal to the curve at P is a(y−1)+(x−1)=0. If the slope of the tangent at any point on the curve is proportional to the ordinate of the point. Determine the equation of the curve
View SolutionThe slope of a curve at any point is the reciprocal of twice the ordinate at that point and it passes through the point(4,3). The equation of the curve is:
View Solution
