If A is the area bounded by the curves y=√1−x2 and y=x3−x , then of πA.
Video Solution
Text Solution
The correct Answer is:2
y=√1−x2 (1)
y=x3−x (2)
y=0 in (2)x=0,1,−1
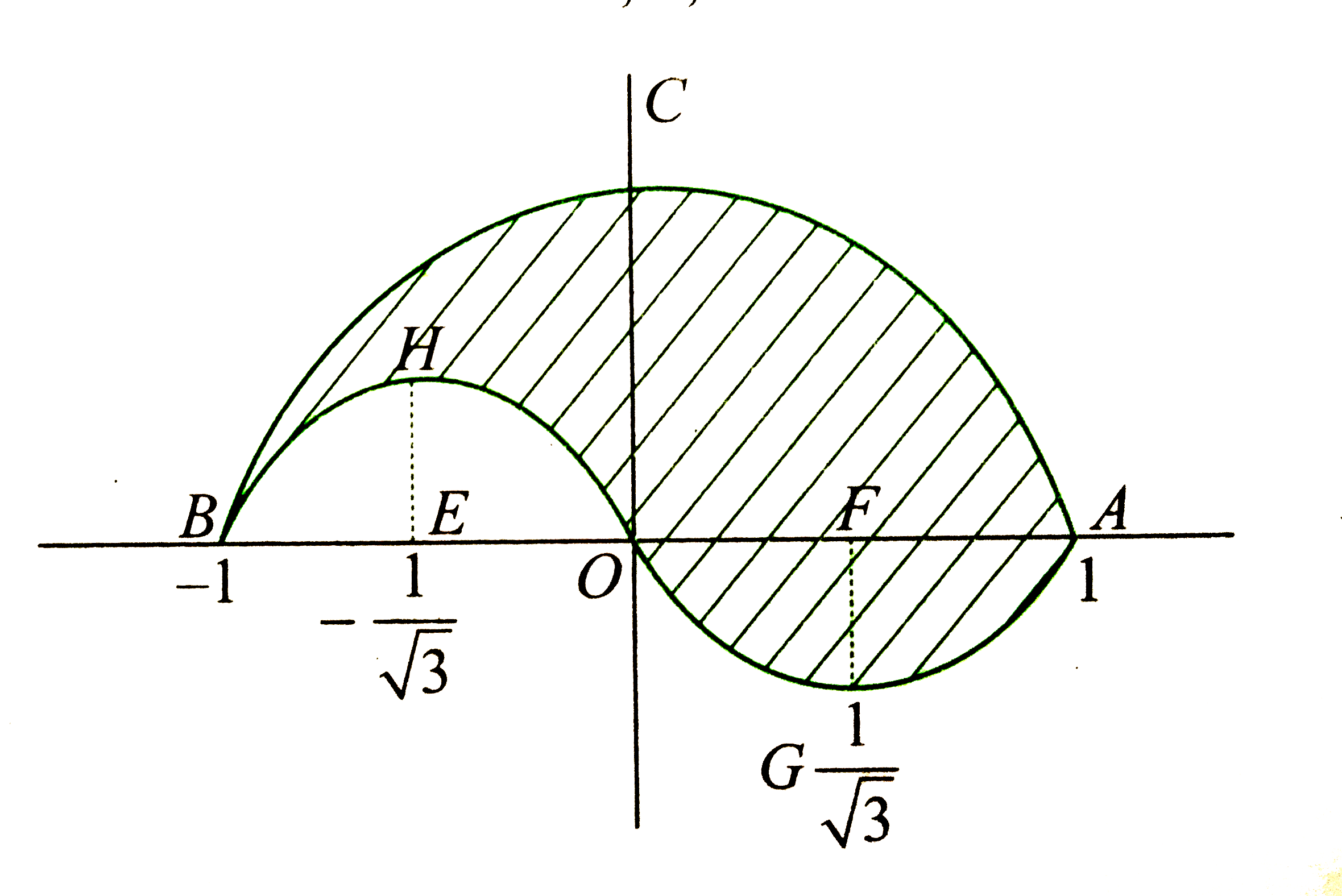
Required area = Area of region BCAGOHB
=Area of semi-circle BCAOB
=π2 (∵ area of BHOEB= area of OFAGO)
|
Topper's Solved these Questions
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Archives
10 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Single Correct Answer Type
30 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Matrix Match Type
5 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
Similar Questions
Find the area bounded by the curves y=6x−x2andy=x2−2x
View SolutionThe area bounded by the curves y=x,y=x3 is
View SolutionFind the area bounded by the curves y=x3−xandy=x2+x.
View SolutionArea bounded by the curves y=x2−1andx+y=3 is:
View SolutionFind area bounded by curves y=√2−x2 and y = |x|.
View SolutionThe area bounded by the curves y=|x|−1 and y=−|x|+1 is
View SolutionFind the area bounded by the curves x+2|y|=1 and x=0 .
View SolutionFind the area bounded by the curves x+2|y|=1 and x=0 .
View SolutionThe area bounded by the curve y=4x−x2 and the x-axis is:
View SolutionFind the area bounded by the curves y=√1−x2 and y=x3−x without using integration.
View Solution
