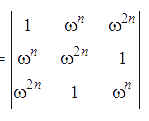Let I, ω and ω2 be the cube roots of unity. The least possible degree of a polynomial, with real coefficients having 2ω2,3+4ω,3+4ω2 and 5−ω−ω2 as roots is -
4
5
6
7
The correct Answer is:B
To find the least possible degree of a polynomial with real coefficients that has the given roots 2ω2, 3+4ω, 3+4ω2, and 5−ω−ω2, we will follow these steps:
Step 1: Identify the roots
The roots provided are:
1. 2ω2
2. 3+4ω
3. 3+4ω2
4. 5−ω−ω2
Step 2: Use properties of cube roots of unity
Recall that the cube roots of unity are 1, ω, and ω2, where:
ω+ω2+1=0⇒ω+ω2=−1
This means ω2=−1−ω and ω=−1−ω2.
Step 3: Find conjugate roots
Since the polynomial must have real coefficients, the complex roots must occur in conjugate pairs.
- If 2ω2 is a root, then 2ω must also be a root because ω and ω2 are conjugates.
- The roots 3+4ω and 3+4ω2 are already conjugate pairs.
- The root 5−ω−ω2 can be simplified using the property of cube roots:
5−ω−ω2=5−(−1)=6
Thus, 6 is also a root.
Step 4: List all the roots
Now we have the following roots:
1. 2ω2
2. 2ω
3. 3+4ω
4. 3+4ω2
5. 6
Step 5: Count the distinct roots
We have identified 5 distinct roots:
- 2ω
- 2ω2
- 3+4ω
- 3+4ω2
- 6
Step 6: Determine the degree of the polynomial
A polynomial with n distinct roots has a degree of n. Since we have 5 distinct roots, the least possible degree of the polynomial is:
Degree=5
Final Answer
The least possible degree of the polynomial with the given roots is 5.
---
The roots provided are:
1. 2ω2
2. 3+4ω
3. 3+4ω2
4. 5−ω−ω2
Recall that the cube roots of unity are 1, ω, and ω2, where:
ω+ω2+1=0⇒ω+ω2=−1
This means ω2=−1−ω and ω=−1−ω2.
Since the polynomial must have real coefficients, the complex roots must occur in conjugate pairs.
- If 2ω2 is a root, then 2ω must also be a root because ω and ω2 are conjugates.
- The roots 3+4ω and 3+4ω2 are already conjugate pairs.
- The root 5−ω−ω2 can be simplified using the property of cube roots:
5−ω−ω2=5−(−1)=6
Thus, 6 is also a root.
Now we have the following roots:
1. 2ω2
2. 2ω
3. 3+4ω
4. 3+4ω2
5. 6
We have identified 5 distinct roots:
- 2ω
- 2ω2
- 3+4ω
- 3+4ω2
- 6
A polynomial with n distinct roots has a degree of n. Since we have 5 distinct roots, the least possible degree of the polynomial is:
Degree=5
The least possible degree of the polynomial with the given roots is 5.
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - Multiple Correct Answer
11 Videos
- COMPLEX NUMBERSBOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CONIC SECTIONSBOOK - CENGAGE ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - All Questions
101 Videos
Similar Questions
Knowledge Check
If 1,ω,ω2 are cube roots of unity then the value of (5+2ω+5ω2)3 is
A27B−9C−27D−81If 1,ω,ω2 are cube roots of unity then the value of (2+2ω−3ω2)3 is
A125B−125C27D−27If 1,ω,ω2 are cube roots of unity then the value of (3+5ω+3ω2)3 is
A6B8C12D16
If 1,ω,ω2 are three cube roots of unity, prove that
(1+ω2)4=ω
View SolutionIf 1,ω,ω2 are three cube roots of unity, prove that
(1−ω)(1−ω2)=3
View SolutionIf 1,ω,ω2 are three cube roots of unity, prove that
ω28+ω29+1=0
View SolutionIf 1,ω,ω2 are three cube roots of unity, prove that
(1−ω−ω2)6=64
View SolutionIf 1,ω,ω2 are the cube roots of unity, prove that
(1+ω)3−(1+ω2)3=0
View Solution