The graph of the quadrationc funtion y=ax2+bx+c is as shown in the following figure.

Now,match the complex numbers given in List I with the corresponding arguments in List II.

Text Solution
The correct Answer is:a→q;b→s;c→p;d→r
Since graph in concave upward , a>0
Grapg intersects y -aixs at negative y -axis. So, c<0
Als, vertex lies to the right of y-axis.
So, −b2a>0. ∴b<0
Complex number a + ib lies in fourth quadrant. ltbr ∴arg(a+ib)=tan−1.ba
Complex number ac - ib lies in thid quadrnt.
∴arg(ac−ib)=−π−tan−1.ba
Complex number -ac+ib lies in first quadrant.
∴arg(−ac+ibc)=−π−tan−1.ba
Complex number abc−ib2 c lies in second quadrant.
∴arg(abc−ib2c)=π+tan−1.ba
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Match the figures in List I, with their corresponding c9ongruence criterion in List II.
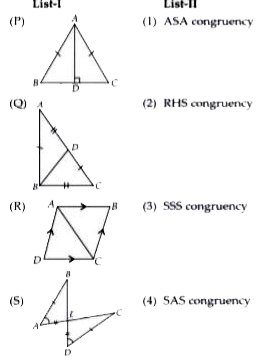 AP-2, Q-4, R-1, S-3BP-3, Q-1, R-2, S-4CP-2, Q-3, R-1, S-4DP-3, Q-4, R-2, S-1
AP-2, Q-4, R-1, S-3BP-3, Q-1, R-2, S-4CP-2, Q-3, R-1, S-4DP-3, Q-4, R-2, S-1 - Question 2 - Select One
Match the compounds given in list I with their characterstics reactions in list II
 A1-a,2-c,3-d,4-bB1-c,2-d,3-b,4-aC1-a,2-b,3-c,4-dD1-d,2-a,3-b,4-c
A1-a,2-c,3-d,4-bB1-c,2-d,3-b,4-aC1-a,2-b,3-c,4-dD1-d,2-a,3-b,4-c - Question 3 - Select One
Match the quantities given in List-I with the units given in List-II
 APQRS4321BPQRS3421CPQRS2314DPQRS1234
APQRS4321BPQRS3421CPQRS2314DPQRS1234
Match the compounds given in list I with their characterstics reactions in list II
 View Solution
View SolutionMatch the statements given in the List-I with the equations given in List-II.
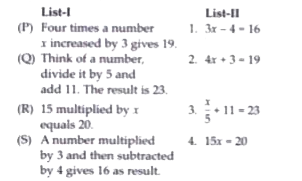 View Solution
View SolutionMatch the quantities given in List-I to the respective ratios given in List-II.
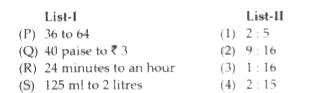 View Solution
View SolutionThe quadratic equation ax2+bx+c=0 has two roots then match the following lists.

Find the correct match from List-I to List-II.View SolutionMatch the statements/expressions given in List I with the values given in List II.
 View Solution
View Solution

