The region represented by the inequality |2z-3i|<|3z-2i| is
the unit disc with its centre at
the exterior of the unit circle with its centre at
the inerior of a square of side units with its centre at
none of these
The correct Answer is:B
To solve the inequality |2z - 3i| < |3z - 2i|, we will follow these steps:
Step 1: Substitute z with x + iy
Let z=x+iy, where x and y are real numbers.
Step 2: Rewrite the inequality
Substituting z into the inequality gives:
|2(x+iy)−3i|<|3(x+iy)−2i|
This simplifies to:
|2x+2iy−3i|<|3x+3iy−2i|
Which can be rewritten as:
|2x+i(2y−3)|<|3x+i(3y−2)|
Step 3: Express the moduli
Now we express the moduli:
√(2x)2+(2y−3)2<√(3x)2+(3y−2)2
Step 4: Square both sides
To eliminate the square roots, we square both sides:
(2x)2+(2y−3)2<(3x)2+(3y−2)2
Expanding both sides:
4x2+(4y2−12y+9)<9x2+(9y2−12y+4)
Step 5: Rearranging the inequality
Rearranging gives:
4x2+4y2−12y+9<9x2+9y2−12y+4
Simplifying this results in:
4x2+4y2+9<9x2+9y2+4
This can be rearranged to:
0<5x2+5y2−5
Dividing through by 5 gives:
0<x2+y2−1
Thus:
x2+y2>1
Step 6: Interpret the result
The inequality x2+y2>1 represents the region outside the circle of radius 1 centered at the origin in the complex plane.
Conclusion
The region represented by the inequality |2z - 3i| < |3z - 2i| is the exterior of the unit circle centered at the origin.
---
Let z=x+iy, where x and y are real numbers.
Substituting z into the inequality gives:
|2(x+iy)−3i|<|3(x+iy)−2i|
This simplifies to:
|2x+2iy−3i|<|3x+3iy−2i|
Which can be rewritten as:
|2x+i(2y−3)|<|3x+i(3y−2)|
Now we express the moduli:
√(2x)2+(2y−3)2<√(3x)2+(3y−2)2
To eliminate the square roots, we square both sides:
(2x)2+(2y−3)2<(3x)2+(3y−2)2
Expanding both sides:
4x2+(4y2−12y+9)<9x2+(9y2−12y+4)
Rearranging gives:
4x2+4y2−12y+9<9x2+9y2−12y+4
Simplifying this results in:
4x2+4y2+9<9x2+9y2+4
This can be rearranged to:
0<5x2+5y2−5
Dividing through by 5 gives:
0<x2+y2−1
Thus:
x2+y2>1
The inequality x2+y2>1 represents the region outside the circle of radius 1 centered at the origin in the complex plane.
The region represented by the inequality |2z - 3i| < |3z - 2i| is the exterior of the unit circle centered at the origin.
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - Multiple Correct Answer
11 Videos
- COMPLEX NUMBERSBOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CONIC SECTIONSBOOK - CENGAGE ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - All Questions
101 Videos
Similar Questions
Knowledge Check
y≥x+2
2x+3y≤6
In which of the following does the shaded region represent the solution set in the xy-plane to the system of inequalities above?A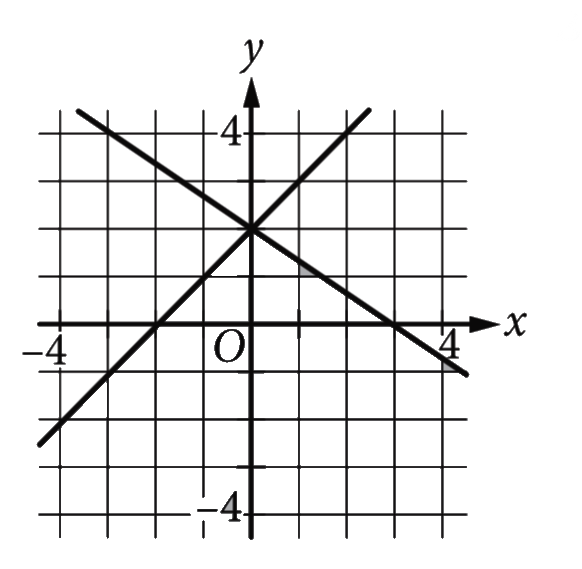 B
B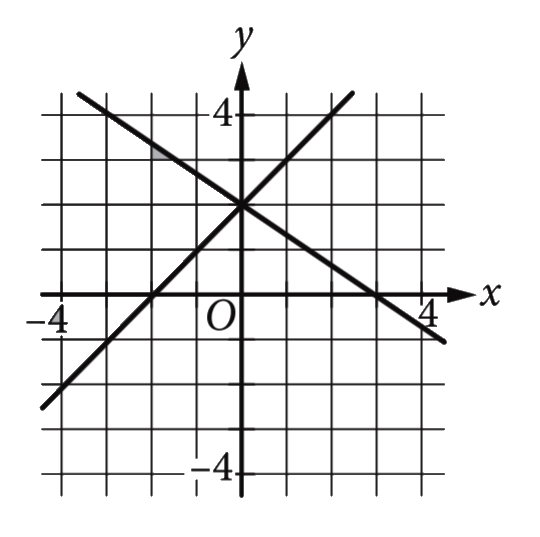 C
C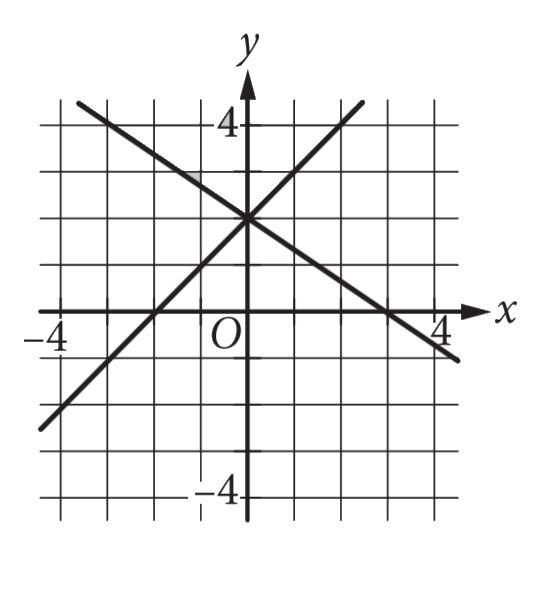 D
D
Illustrate and explain the region of the Argand's plane represented by the inequality |z+i|≥|z+2|
View SolutionThe locus represented by the equation |z−1|=|z−i| is
View SolutionPlot the region represented by π3≤arg(z+1z−1)≤2π3 in the Argand plane.
View SolutionShade the region given by inequality
2x+y≥6
View SolutionFind the center of the are represented by arg[(z−3i)/(z−2i+4)]=π/4 .
View SolutionThe locus represented by |z-1|=|z+i| is:
View SolutionLet the center of the circle represented by z¯z−(2+3i)z−(2−3i)¯z+9=0'be(x,y), then the value of x2+y2+xy is
View Solution
