The line xa+yb=1 meets the x-axis at A, the y-axis at B, and the line y=x at C such, that the area of DeltaAOC is twice the area of DeltaBOC . Then the coordinates of C are (b3,b3) (b) (2a3,2a3) (c) (2b3,2b3) (d) none of these
(b3,b3)
(2a3,2a3)
(2b3,2b3)
none of these
The correct Answer is:C
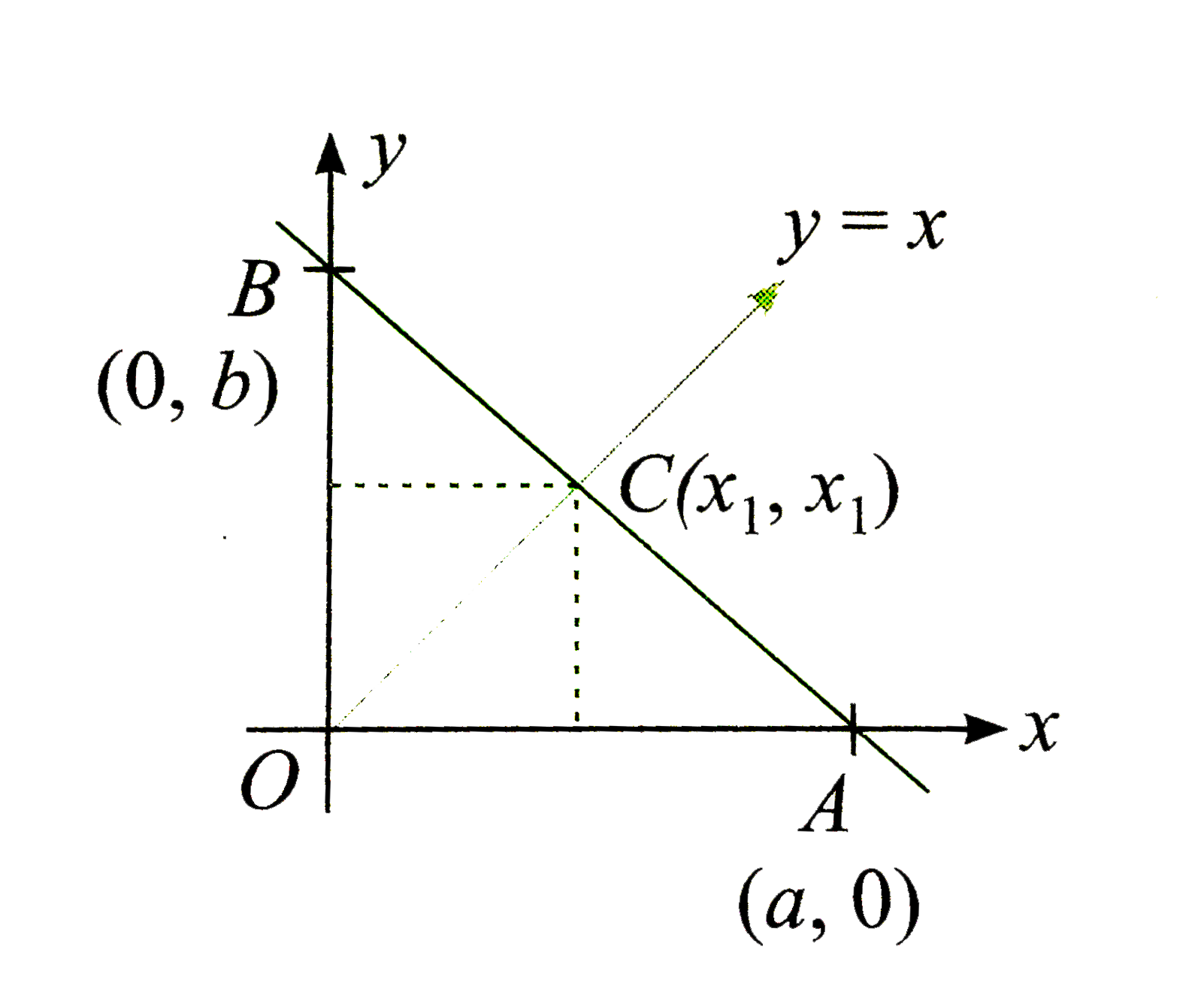
Given arΔAOC=2(arΔBOC)
or12(OA)(x1)=2×12(OB)(x1)
or a=2b
The equation of AB is
xa+yb=1 (1)
or x2b+yb=1 (2)
Since point C lies on line (2), we have
x12b+x1b=1
or x1=2b3=a3
or C≡(2b3,2b3)
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)30videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)27videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.65videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
The area of a parallelogram formed by the lines ax±by±c=0 is (a)c2(ab) (b) 2c2(ab) (c)c22ab (d) none of these
View SolutionThe area of a parallelogram formed by the lines ax±bx±c=0 is (a) c2(ab) (b) 2c2(ab) (c) c22ab (d) none of these
View SolutionThe line 2x+3y=12 meets the x-axis at A and y-axis at B. The line through (5,5) perpendicular to AB meets the x-axis and the line AB at C and E respectively. If O is the origin of coordinates, find the area of figure OCEB.
View SolutionThe line 3x+2y=24 meets the y-axis at A and the x-axis at B. The perpendicular bisector of AB meets the line through (0,−1) parallel to the x-axis at C. If the area of triangle ABC is A , then the value of A13 is________
View SolutionThe line 3x+2y=24 meets the y-axis at A and the x-axis at B. The perpendicular bisector of AB meets the line through (0,−1) parallel to the x-axis at C. If the area of triangle ABC is A , then the value of A13 is________
View SolutionThe straight lines 4ax+3by+c=0 , where a+b+c are concurrent at the point a) (4,3) b) (14,13) c) (12,13) d) none of these
View SolutionThe straight lines 4ax+3by+c=0 passes through? , where a+b+c=0 (a)(4,3) (b) (14,13) (12,13) (d) none of these
View SolutionIf a,b,c are in G.P. write the area of the triangle formed by the line ax+by+c=0 with the coordinates axes.
View SolutionA plane meets the coordinate axes at A, B, C such that the centroid of ΔABC is the point (a, b, c) . If the equation of the plane is xa+yb+zc=k, then k= 1 b. 2 c. 3 d. none of these
View SolutionThe equation of the base of an equilateral triangle ABC is x+y=2 and the vertex is (2,−1) . The area of the triangle ABC is: √26 (b) √36 (c) √38 (d) None of these
View Solution
