Question

The line $\frac{x}{3}+\frac{y}{4}=1$
meets the y-axis
and x-axis at A and B
respectively. A square $ABCD$
is constructed on the line segment $AB$
away from the origin. The coordinates of the vertex of the square
farthest from the origin are

Options

A. 7,3
B. 4,7
C. 6,4
D. 3,8

Answer

B

Explanation

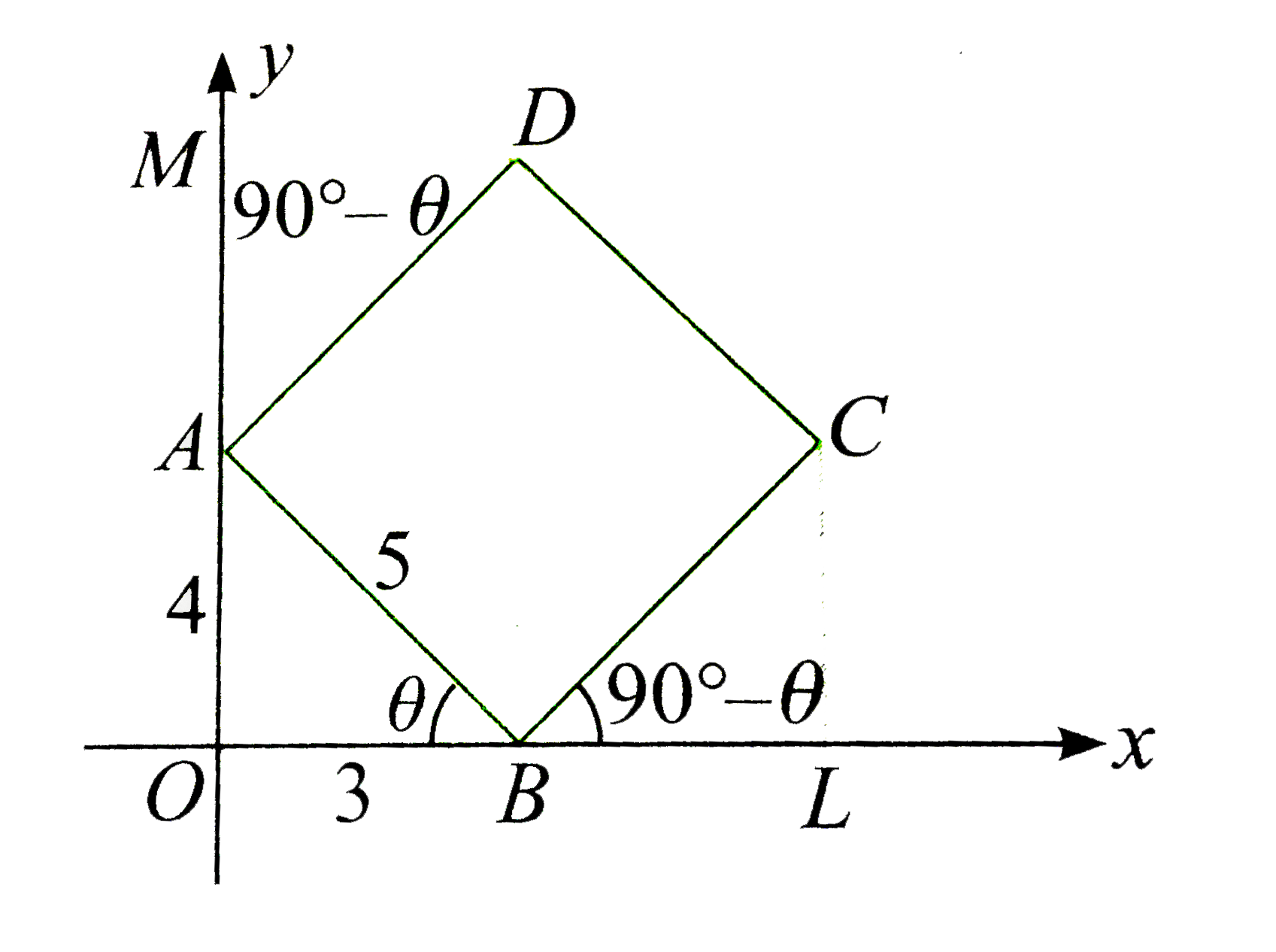
The coordinates of A are (0,4) and those of B are (3,0).
`BC=AB=sqrt(3^(2)+4^(2)) = 5`
`"or " BL=BC "sin" theta "and " CL=BC "cos" theta`
`"or " BL=5 xx (4)/(5) = 4 "and"`
`CL=5 xx (3)/(5) = 3`
Similarly, MD =4 and AM=3.
So, the coordinates of C are (OB+BL,CL) `-=(7,3)` and those of D are (MD, OA+AM) `-=(4,7)`.
The coordinates of the vertex farthest from the origin are (4,7).