(a) Resistors given as R1,R2andR3 are connected in series to a battery V. Draw the circuit diagram showing the arrangement. Derive an expression for the equivalent resistance of the combination.
(b) If R1=10Ω,R2=20ΩandR3=30Ω, calculate the effective resistance when they are connected in series to a battery of 6 V. Also find the current flowing in the circuit.
Solution:
(a) To draw the circuit diagram for resistors R1,R2, and R3 connected in series to a battery V:
1. Draw the Battery: Start by drawing a battery symbol, which consists of two parallel lines (one longer and one shorter).
2. Connect Resistors in Series: Draw three resistors in a straight line connected one after the other. Label them as \( R_1, R_2, \) and \( R_3 \).
3. Indicate Current Flow: Draw arrows to indicate the direction of current flow from the positive terminal of the battery through the resistors and back to the negative terminal.
The circuit diagram will look like this:
+⊢−R1−−−R2−−−R3−−−|−⊢−−−−−−−−−−−−−−−−−−−−−−−|
Deriving the Expression for Equivalent Resistance:
1. Understanding Series Connection: In a series circuit, the same current \( I \) flows through each resistor.
2. Applying Ohm's Law: For each resistor, we can write:
- \( V_1 = I R_1 \)
- \( V_2 = I R_2 \)
- \( V_3 = I R_3 \)
3. Total Voltage: The total voltage \( V \) across the series combination is the sum of the voltages across each resistor:
\(
V = V_1 + V_2 + V_3
\)
Substituting the expressions from Ohm's Law:
\(
V = I R_1 + I R_2 + I R_3
\)
4. Factoring Out Current: Factoring out \( I \) from the right-hand side gives:
\(
V = I (R_1 + R_2 + R_3)
\)
5. Expression for Equivalent Resistance: From Ohm's Law, we also know that \( V = I R \), where \( R \) is the equivalent resistance. Thus, we can equate:
\(
I R = I (R_1 + R_2 + R_3)
\)
Since \( I \) is common and non-zero, we can simplify to:
\(
R = R_1 + R_2 + R_3
\)
Thus, the expression for the equivalent resistance \( R \) of resistors in series is:
\(
R = R_1 + R_2 + R_3
\)
---
(b) Given \( R_1 = 10 \, \Omega \), \( R_2 = 20 \, \Omega \), and \( R_3 = 30 \, \Omega \):
1. Calculate the Equivalent Resistance:
\(
R = R_1 + R_2 + R_3 = 10 + 20 + 30 = 60 \, \Omega
\)
2. Calculate the Current Flowing in the Circuit:
Using Ohm's Law \( V = I R \):
- Given \( V = 6 \, V \) and \( R = 60 \, \Omega \):
\(
6 = I \times 60
\)
Rearranging gives:
\(
I = \frac{6}{60} = 0.1 \, \text{A}
\)
Final Answers:
- The equivalent resistance \( R \) is \( 60 \, \Omega \).
- The current flowing in the circuit is \( 0.1 \, \text{A} \).
---
2. Connect Resistors in Series: Draw three resistors in a straight line connected one after the other. Label them as \( R_1, R_2, \) and \( R_3 \).
3. Indicate Current Flow: Draw arrows to indicate the direction of current flow from the positive terminal of the battery through the resistors and back to the negative terminal.
2. Applying Ohm's Law: For each resistor, we can write:
- \( V_1 = I R_1 \)
- \( V_2 = I R_2 \)
- \( V_3 = I R_3 \)
\(
V = V_1 + V_2 + V_3
\)
Substituting the expressions from Ohm's Law:
\(
V = I R_1 + I R_2 + I R_3
\)
\(
V = I (R_1 + R_2 + R_3)
\)
\(
I R = I (R_1 + R_2 + R_3)
\)
Since \( I \) is common and non-zero, we can simplify to:
\(
R = R_1 + R_2 + R_3
\)
\(
R = R_1 + R_2 + R_3
\)
\(
R = R_1 + R_2 + R_3 = 10 + 20 + 30 = 60 \, \Omega
\)
Using Ohm's Law \( V = I R \):
- Given \( V = 6 \, V \) and \( R = 60 \, \Omega \):
\(
6 = I \times 60
\)
Rearranging gives:
\(
I = \frac{6}{60} = 0.1 \, \text{A}
\)
- The equivalent resistance \( R \) is \( 60 \, \Omega \).
- The current flowing in the circuit is \( 0.1 \, \text{A} \).
Similar Questions
You are given two resistance R1=(4.0±0.1)Ω and R2=(9.1±0.2)Ω. Calculate their effective resistance when they are connected (i) in series and (ii) in parallel. Also calculate the percentage error in each case.
View SolutionTwo coils of resistances R1=3ΩandR2=6.Ωare connected in series across a battery of p.d. 12 V. Draw the circuit diagram. Find :
the total electrical energy supplied by the battery in 1 minute.
View Solution
Knowledge Check
Two resistors of resistances R1=(300±3)Ω and R2=(500±4)Ω are connected in series. The equivalent resistance of the series combination is
A(800±1)ΩB(800±7)ΩC(200±7)ΩD(200±1)Ω
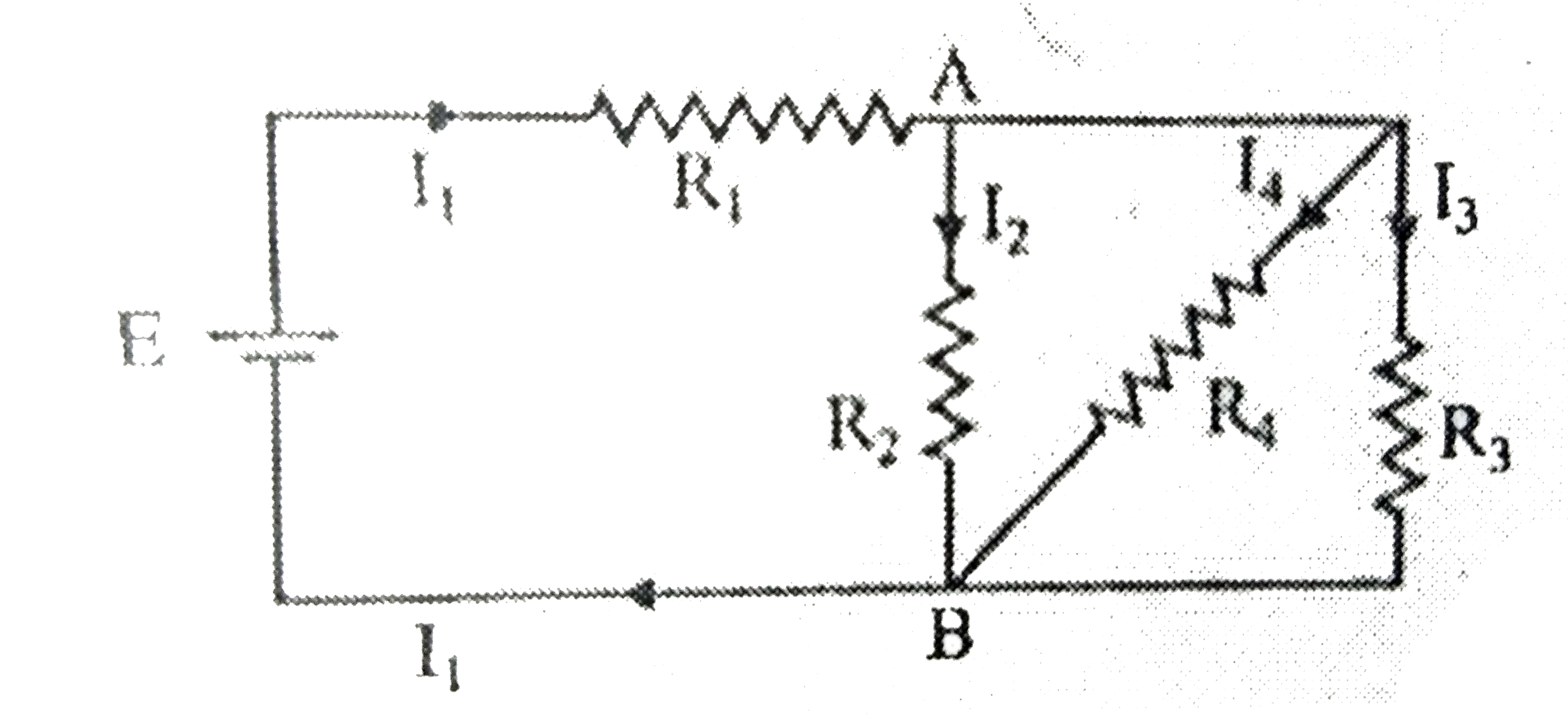
In the circuit shown, R1=4Ω,R2=R3=15Ω,R4=30ΩandE=10V. Caculate the equivalent resistance of te circuit and the current in each resistor.
View SolutionIf in Fig. 12.12, R1=10Ω,R2=40Ω,R3=30Ω,R5=60Ω, and a 12 V battery is connected to the arrangemtn. Calculate (a) the total resistance in the circuit, and (b) the total current flowing in the circuit.
View SolutionIn the circuit shown, R1=2Ω,R2=R3=10Ω,R4=20ΩandE=6V. Work out the equivalent resistance of the circuit and the current in each resistor.
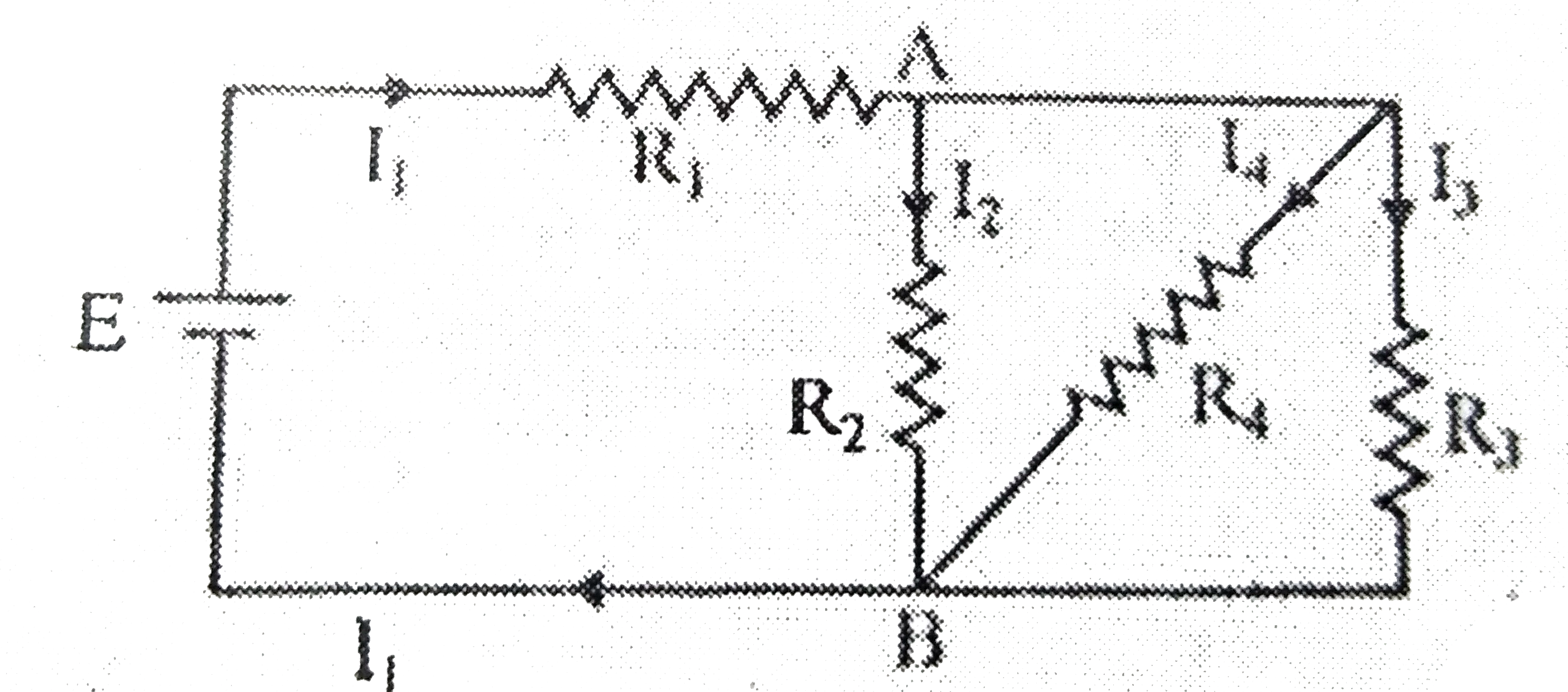
View SolutionA 6 V, 12 W lamp is connected in series with a resistor R and a source of voltage 12 V.
What is the current flowing through the circuit?
View SolutionThe potential difference in volt across the resistance R3 in the circuit shown in figure, is (R1=15Ω,R2=15Ω,R3=30Ω,R4=35Ω)
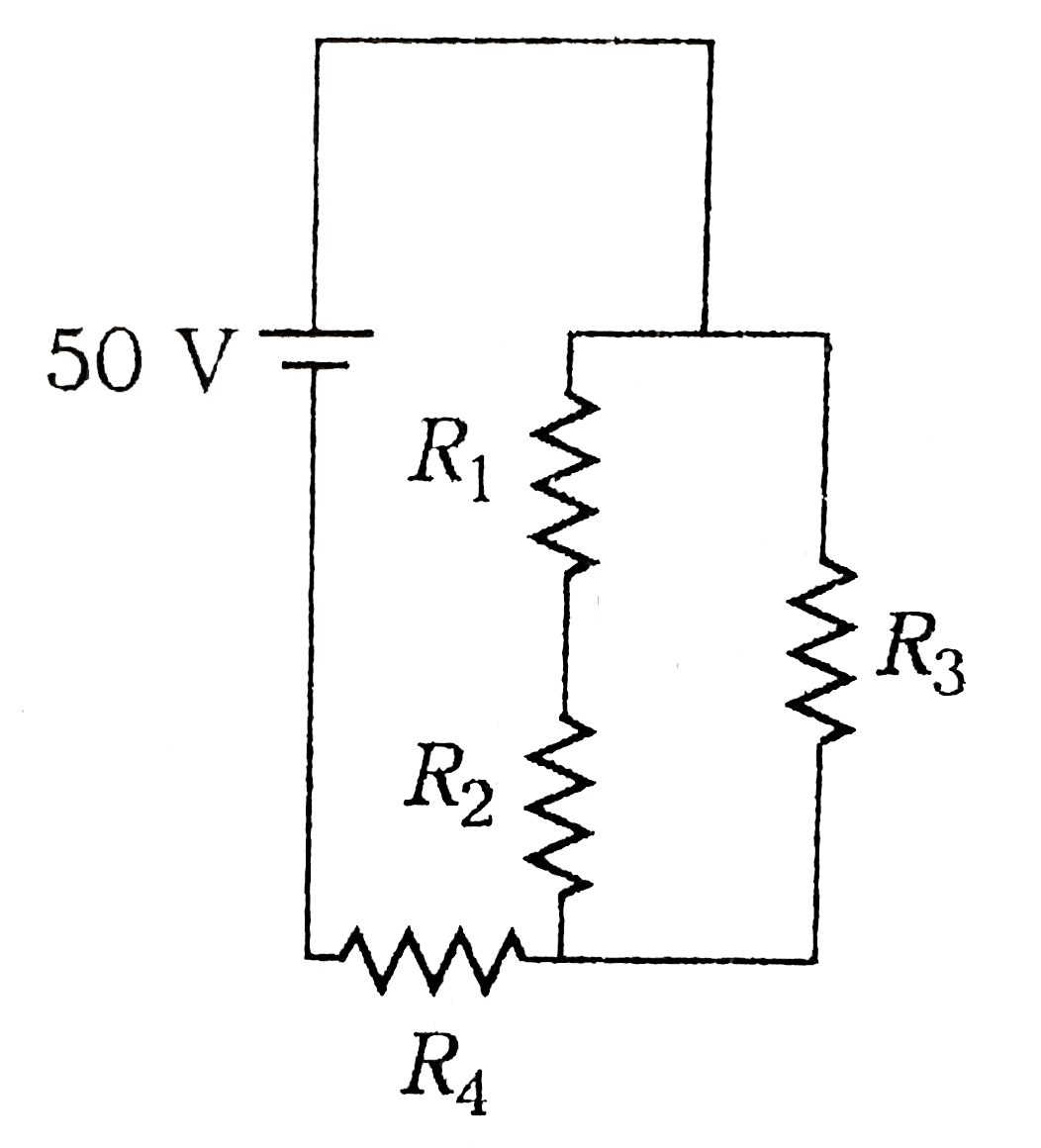
View SolutionIn the circuit shown, R1=2Ω,R2=R3=10ΩandE=6V. Work out the equivalent resistance of the circuit and the current in each resistor.
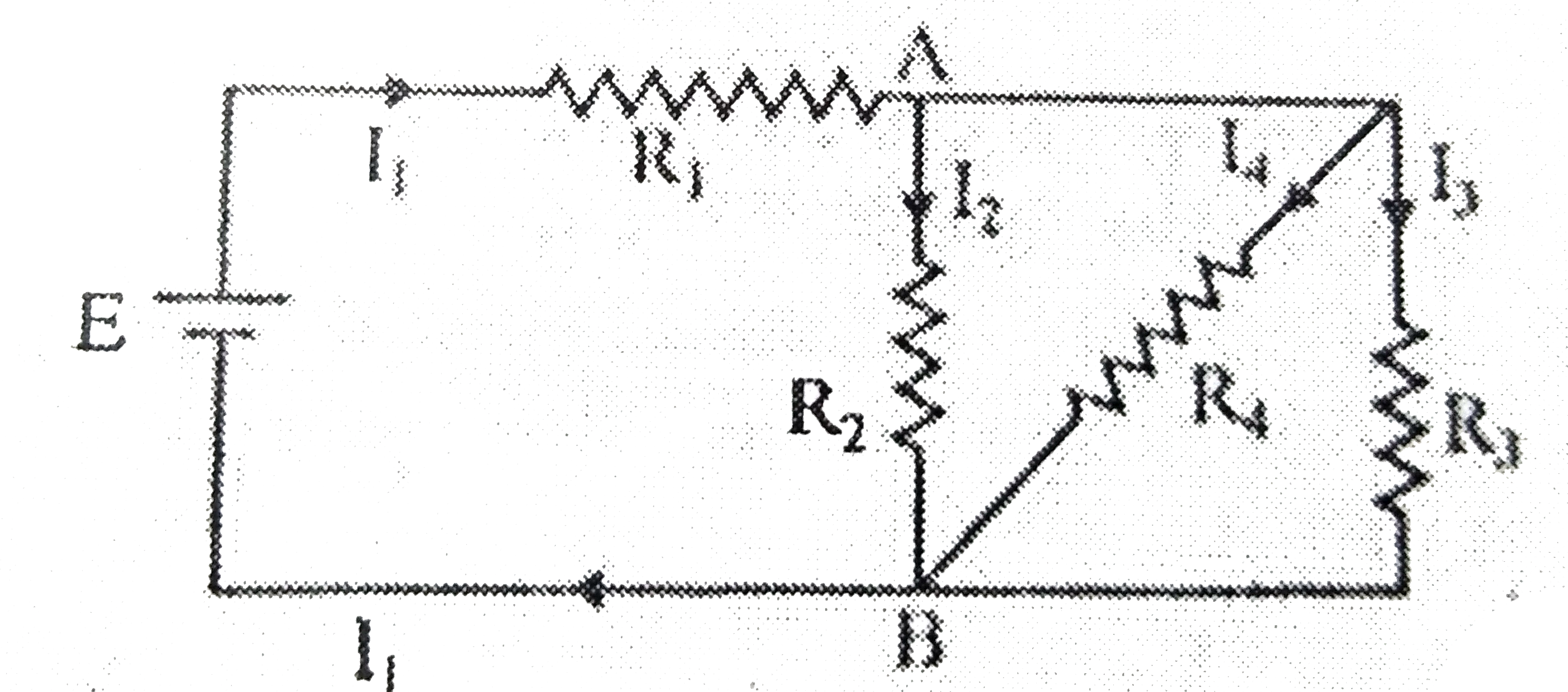
View SolutionIn the given circuit, R1 = 10Ω R2=6Ω and E = 10V, then correct statement is
View Solution
