Two coils of resistances R1=3ΩandR2=6.Ωare connected in series across a battery of p.d. 12 V. Draw the circuit diagram. Find :
the total electrical energy supplied by the battery in 1 minute.
To solve the problem step by step, we will follow these instructions:
Step 1: Draw the Circuit Diagram
We have two resistors, \( R_1 = 3 \, \Omega \) and \( R_2 = 6 \, \Omega \), connected in series across a battery with a potential difference of \( 12 \, V \).
Circuit Diagram:
±−−(R1=3Ω)−−−(R2=6Ω)−−−+∣|||(Baery:12V)|||±−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−+
Step 2: Calculate the Total Resistance
Since the resistors are connected in series, the total resistance \( R_f \) is given by the sum of the individual resistances:
\(
R_f = R_1 + R_2 = 3 \, \Omega + 6 \, \Omega = 9 \, \Omega
\)
Step 3: Calculate the Total Electrical Energy Supplied by the Battery
The total electrical energy \( E \) supplied by the battery can be calculated using the formula:
\(
E = \frac{V^2 \cdot t}{R_f}
\)
where:
- \( V = 12 \, V \) (potential difference)
- \( t = 60 \, s \) (time in seconds)
- \( R_f = 9 \, \Omega \) (total resistance)
Substituting the values:
\(
E = \frac{(12 \, V)^2 \cdot (60 \, s)}{9 \, \Omega}
\)
Calculating the values:
\(
E = \frac{144 \cdot 60}{9}
\)
\(
E = \frac{8640}{9} = 960 \, J
\)
Final Answer
The total electrical energy supplied by the battery in 1 minute is \( 960 \, J \).
---
We have two resistors, \( R_1 = 3 \, \Omega \) and \( R_2 = 6 \, \Omega \), connected in series across a battery with a potential difference of \( 12 \, V \).
±−−(R1=3Ω)−−−(R2=6Ω)−−−+∣|||(Baery:12V)|||±−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−+
Since the resistors are connected in series, the total resistance \( R_f \) is given by the sum of the individual resistances:
\(
R_f = R_1 + R_2 = 3 \, \Omega + 6 \, \Omega = 9 \, \Omega
\)
The total electrical energy \( E \) supplied by the battery can be calculated using the formula:
\(
E = \frac{V^2 \cdot t}{R_f}
\)
where:
- \( V = 12 \, V \) (potential difference)
- \( t = 60 \, s \) (time in seconds)
- \( R_f = 9 \, \Omega \) (total resistance)
\(
E = \frac{(12 \, V)^2 \cdot (60 \, s)}{9 \, \Omega}
\)
\(
E = \frac{144 \cdot 60}{9}
\)
\(
E = \frac{8640}{9} = 960 \, J
\)
The total electrical energy supplied by the battery in 1 minute is \( 960 \, J \).
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(A)
43 Videos
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(A) ( MULTIPLE CHOICE TYPE)
2 Videos
- CALORIMETRYBOOK - ICSECHAPTER - CALORIMETRYEXERCISE - EXERCISE-11(B) (NUMERICALS)
15 Videos
- ELECTRO-MAGNETISM BOOK - ICSECHAPTER - ELECTRO-MAGNETISM EXERCISE - EXERCISE-10 (C) NUMERICALS
1 Video
Similar Questions
Two resistors R1andR2 of resistance 3 Ω and 6 Ωrespectively are connected in parallel across a battery of p.d. 12 V. Draw the circuit diagram. Calculate the electrical energy consumed in 1 minute in each resistance.
View SolutionFig. shows two resistors A of 4Ω and B of 6 Ω joined in series to a battery of e.m.f. 12 V and internal resistance 2 Ω . Calculate :
the electrical energy spent in 1 minute in resistor A
View Solution
Knowledge Check
Two resistors of resistances R1=(300±3)Ω and R2=(500±4)Ω are connected in series. The equivalent resistance of the series combination is
A(800±1)ΩB(800±7)ΩC(200±7)ΩD(200±1)ΩTwo resistances R1=100±3ΩandR2=200±4Ω are connected in series . Find the equivalent resistance of the series combination.
A(66.7±1.8)ΩB(66.7±4.0)ΩC(66.7±3.0)ΩD(66.7±7.0)Ω
Two resistances R1=100±3ΩandR2=200±4Ω are connected in series . Find the equivalent resistance of the series combination.
View Solutiontwo heading coils of resistances 10Ωand20Ω are connected in parallel and connected to a battery of emf 12 V and internal resistance 1Ω Thele power consumed by the n are in the ratio
View SolutionAn inductor of inductance L = 400 mH and resistors of resistance R1=2Ω and R2=2Ω are connected to a battery of emf 12 V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at t=0. The potential drop across L as a function of time is
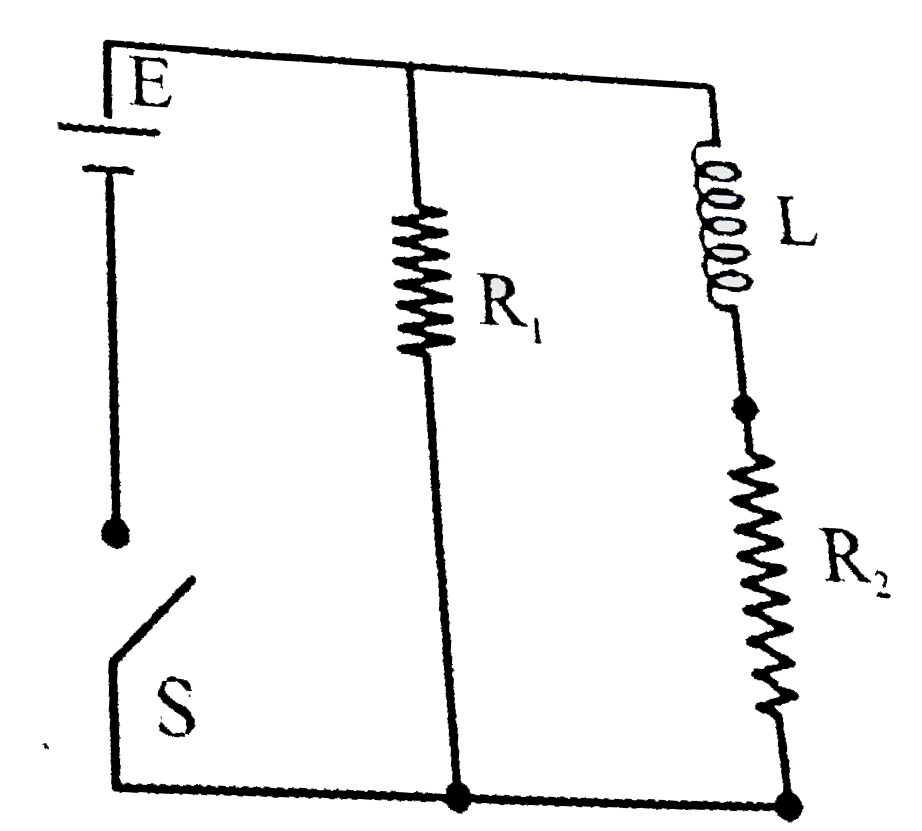
View SolutionAn inductor of inductance L = 400 mH and resistors of resistance R1=2Ω and R2=2Ω are connected to a battery of emf 12 V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at t=0. The potential drop across L as a function of time is

View SolutionAn inductor of inductance L = 400 mH and resistors of resistance R1=2Ω and R2=2Ω are connected to a battery of emf 12 V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at t=0. The potential drop across L as a function of time is

View SolutionFig. shows two resistors A of 4Ω and B of 6 Ω joined in series to a battery of e.m.f. 12 V and internal resistance 2 Ω . Calculate :

the current in circuit,
View Solution
