write the expression for the generalized form of Ampere's circuital law. Discuss its significance and describe briefly how the concept of dislacement current is explained through charing/discharging of a capacitor in an electric circuit.
Step-by-Step Solution
Step 1: Write the expression for the generalized form of Ampere's Circuital Law.
The generalized form of Ampere's Circuital Law can be expressed mathematically as:
∮B⋅dl=μ0(I+ϵ0dΦEdt)
Where:
- ∮B⋅dl is the line integral of the magnetic field B around a closed loop.
- μ0 is the permeability of free space.
- I is the conduction current passing through the loop.
- ϵ0 is the permittivity of free space.
- dΦEdt is the rate of change of electric flux through the surface enclosed by the loop.
Step 2: Discuss the significance of this law.
The significance of the generalized form of Ampere's Circuital Law lies in its ability to account for situations where electric fields change over time. This is crucial in understanding electromagnetic phenomena where both electric and magnetic fields interact. It extends Ampere's original law, which only considered steady currents, to include the effects of changing electric fields, thus providing a more complete description of electromagnetism.
Step 3: Explain the concept of displacement current through charging/discharging of a capacitor.
When a capacitor is charged, an electric field is established between its plates. Although there is no physical current flowing through the dielectric material between the plates, the changing electric field creates a displacement current. This displacement current can be thought of as a "current" that arises due to the changing electric field in the dielectric medium.
- Charging a Capacitor: When a voltage is applied, charges accumulate on the plates of the capacitor, creating an electric field. The rate of change of this electric field contributes to the displacement current, allowing Ampere's law to apply even in regions where there is no conduction current.
- Discharging a Capacitor: When the capacitor discharges, the stored energy is released, and the electric field between the plates decreases. Again, the changing electric field leads to a displacement current, which can be analyzed using the generalized Ampere's law.
This concept of displacement current is essential for understanding how electric fields and magnetic fields interact in circuits involving capacitors, especially in AC circuits where the fields are constantly changing.
- ∮B⋅dl is the line integral of the magnetic field B around a closed loop.
- μ0 is the permeability of free space.
- I is the conduction current passing through the loop.
- ϵ0 is the permittivity of free space.
- dΦEdt is the rate of change of electric flux through the surface enclosed by the loop.
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - section -D
3 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - section -E
6 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - section B
4 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
Using Ampere's circuital law, obtain an expression for the magnetic field along the axis of a current carrying solenoid of length l and having N number of turns.
View SolutionConsidering the case of a parallel plate capacitor being charged, show how one is required to generalize Ampere's circuital law to include the term due to displacment current.
View SolutionA capacitor is charged to a certain potential and then allowed to discharge through a resistance R. The ratio of charge on the capacitor to current in the circuit
View SolutionHow does Ampere-Maxwell law explain the flow the of current through a capacitor when it is being charged by a battery? Write the expression for the displacement current in terms of the rate of change of electric flux.
View SolutionWrite Maxwell's generalization of Ampere's Circuital Law. Show that in the process of charging a capacitor the , current produced within the plates of the capcitor is I=ε0=dΦEdt where ΦE is the electric flux produced during charging of the capacitor plates.
View Solution(a) Write, using Biot-Savart law, the expression for the magnetic field →B due to an element →dl carrying current I at a distance →r from it in a vector form.
Hence ,derive the expression for the magnetic field due to a current carring loop of radius R at a point P distant x from its centre along the axis of the loop.
View Solution(a) In a series LCR circuit connected across an AC source of variable frequency, obtain the expression for its impedance and draw a plot showing its variation with frequency of the AC source.
(b) What is the phase difference between the voltages across inductor and the capacitor at resonance in the LCR circuit ?
(c ) When and inductor is connected to a 200 V DC voltage, a current of 1Aflows trough it. when the same inductor is connected to a 200 V, 50 Hz AC source, only 0.5 A current flows. Explain, why ? Also, calculate the self inductance of the inductor.
View SolutionExplain, with the help of a circuit diagram, the working of a photo diaode. Write briefly how it is used to detect the optical signals.
View SolutionHow many time constants will elapse before the charge on a capacitor falls to 0.1%of its maximum value in a discharging RC circuit.
View SolutionA part of an electric circuit is shown in figure.
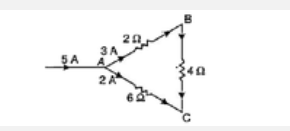
Using Kirchhoff.s 2nd law, find the current I flowing through the 4Ω resistor.
View Solution
