Question

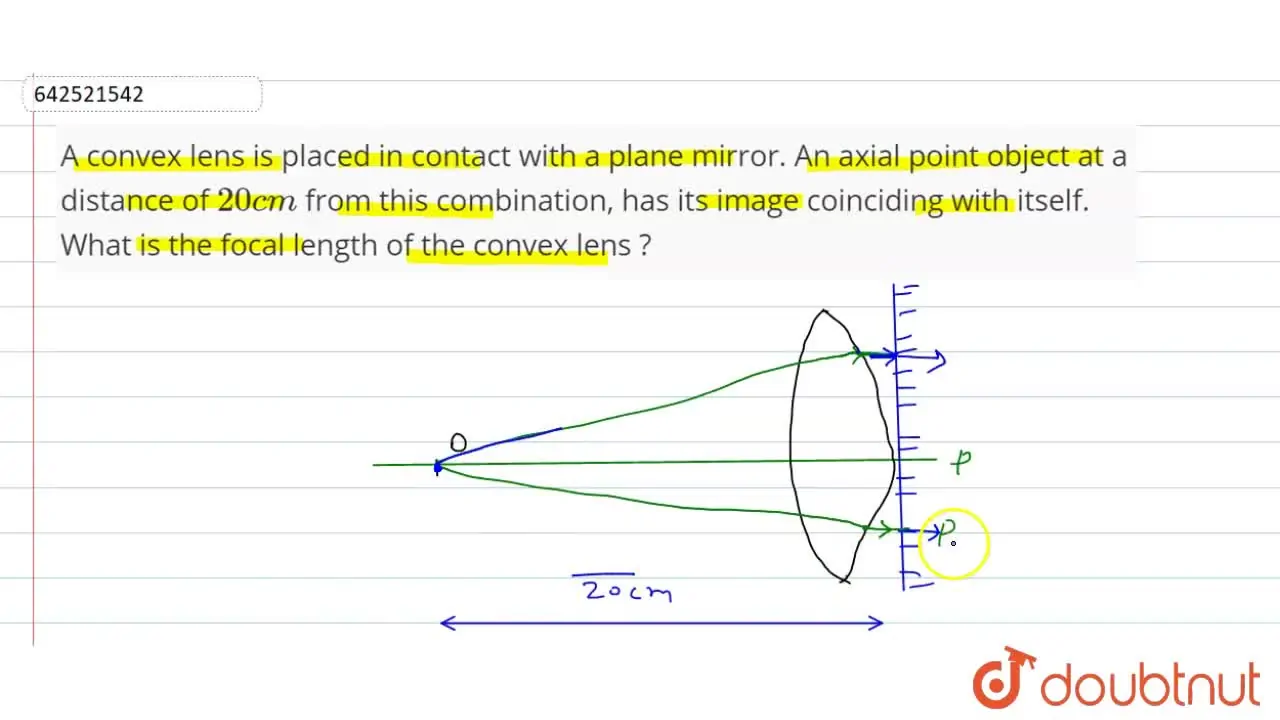
A convex lens is placed in contact with a plane mirror. An axial point object at a distance of $20cm$ from this combination, has its image coinciding with itself. What is the focal length of the convex lens ?

Explanation

To solve the problem, we need to analyze the situation where a convex lens is placed in contact with a plane mirror, and an object is placed at a distance of 20 cm from this combination. The image formed coincides with the object itself, indicating that the image distance (v) is equal to the object distance (u) but with a negative sign, since the image is virtual.

1. Understanding the Setup:
- We have a convex lens in contact with a plane mirror.
- An object is placed 20 cm away from the lens-mirror combination.

2. Identify Object and Image Distances:
- Let the object distance (u) be -20 cm (the negative sign indicates that the object is on the same side as the incoming light).
- Since the image coincides with the object, the image distance (v) is also -20 cm.

3. Using the Lens Formula:
The lens formula is given by:
\( \frac{1}{f} = \frac{1}{v} - \frac{1}{u} \)
where \( f \) is the focal length of the lens.

4. Substituting Values:
- Substitute \( u = -20 \) cm and \( v = -20 \) cm into the lens formula:
\( \frac{1}{f} = \frac{1}{-20} - \frac{1}{-20} \)
\( \frac{1}{f} = -\frac{1}{20} + \frac{1}{20} = 0 \)

5. Finding Focal Length:
- Since \(\frac{1}{f} = 0\), it implies that:
\( f = \infty \)
This means that the focal length of the convex lens is effectively infinite.

Conclusion:
The focal length of the convex lens in this configuration is infinite.