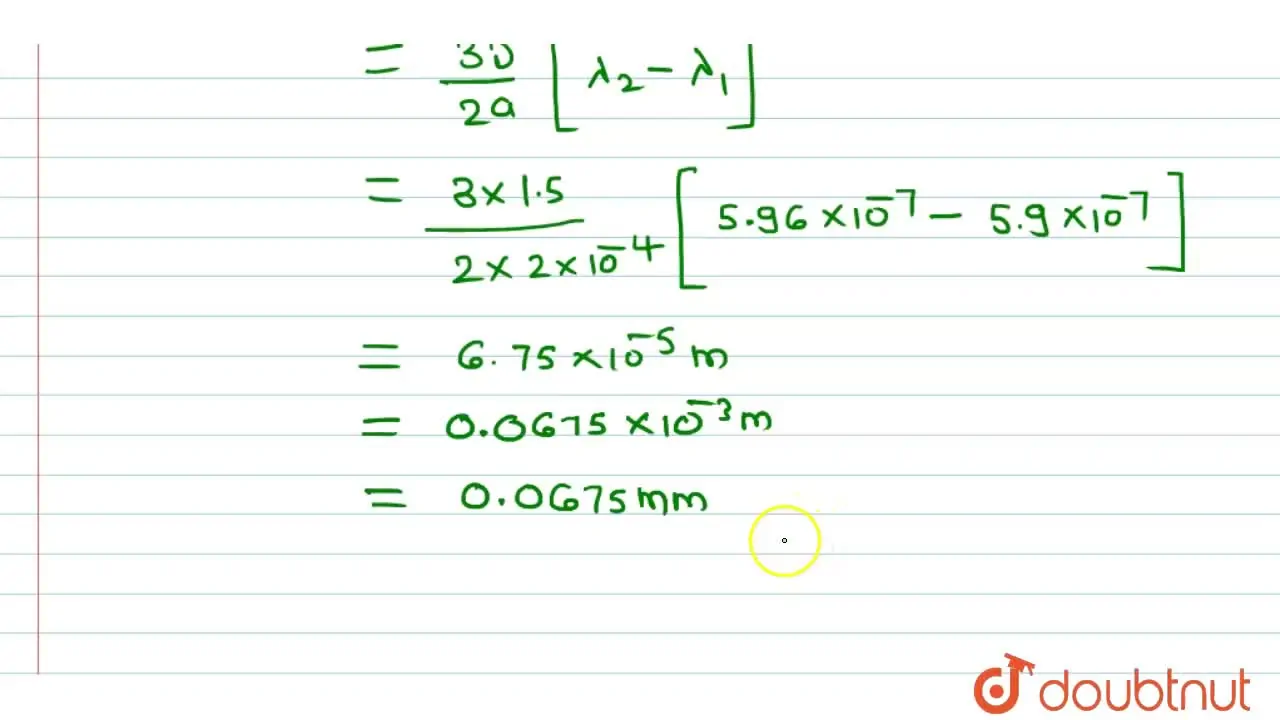Two wavelengths of sodium light 590 nm and 596 nm are used, in turn, to study the diffraction taking place at a single slit of aperture 2×10−4m. The distance between the slit and the screen is 1.5 m. Calculate the separation between the positions of the first maxima of the diffraction pattern obtained in the two cases.
(a) If the width of each slit is comparable to the wavelength of light used, the interference pattern thus obtained in the double slit experiment is modified by diffraction from each of two slits.
(b) Given that : Wavelength of the light beam,
λ1=590nm=5.9×10−7m
Wavelength of another light beam,
λ2=596nm=5.96×10−7m
Distance of the slits from the screen = D = 1.5 m
Distance between the two slits =a=2×10−4m
For the first secondry maxima,
sinθ=3λ12a=x1D OR x1=3λ1D2aandx2=3λ2D2a
∴ Spacing between the positions of first secondary maxima of two sodium lines
x1−x2=3D2a(λ2−λ1)=6.75×10−5m.
Related Playlists
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET - II (Delhi Board)7videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET - III (Delhi Board)6videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - PHYSICS (Theory) [SET - III]9videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
Two wavelengths of sodium light 590 nm and 596 nm are used , in turn, to study the diffraction taking place due to a single slit of aperture 1×10−4m. The distance between the slit and the screen is 1.8m. Calculate the separation between the positions of the first maxima of the diffraction pattern obtained in the two cases.
View SolutionTwo wavelengths of sodium light of 590 nm and 596 nm are used in turn to study the diffraction taking place at a single slit of aperture 2×10−6m. The distance between the slit and the screen is 1.5 m. Calculate the separation between the positions of first maxima of the diffraction pattern obtained in the two cases.
View SolutionTwo wavelengths of sodium light 590 nm and 596 nm are used in turn to study the diffraction at a single slit of size 4mm. The distance between the slit and screen is 2m. Calculate the separation between the positions of the first maximum of the diffraction pattern obtained in the two cases.
View SolutionIn a YDSE, distance between the slits and the screen is 1m, separation between the slits is 1mm and the wavelength of the light used is 5000nm. The distance of 100th maxima from the central maxima is:
View SolutionA screen is placed at 50cm from a single slit, which is illuminated with 600nm light. If separation between the first and third minima in the diffraction pattern is 3.0mm, then width of the slit is:
View SolutionIn YDSE, separation between slits is 0.15 mm, distance between slits and screen is 1.5 m and wavelength of light is 589 nm, then fringe width is
View SolutionIn YDSE, separation between slits is 0.15 mm, distance between slits and screen is 1.5 m and wavelength of light is 589 nm, then fringe width is
View SolutionIn a single slit diffraction method, the distance between slit and screen is 1m. The size of the slit is 0.7mm and second maximum is formed at the distance of 2mm from the centre of the screen, then find out the wavelength of light.
View SolutionA source emitting light of wavelengths 480 nm and 600 nm is used in a double slit interference experiment. The separation between the slits is 0.25 mm and the interference is observed on a screen placed at 150 cm from the slits. Find the linear separation between the first maximum (next to the central maximum) corresponding to the two wavelengths.
View SolutionWhat is the value of angular fringe width if fringe width is = 0.4 nm and separation between slit and screen is 2m.
View Solution