A cell of emf 'E' and internal resistance 'r' draws a current 'I'. Write the relation between terminal voltage 'V' in terms of E, I and r.
To derive the relation between terminal voltage V, electromotive force (emf) E, current I, and internal resistance r of a cell, we can follow these steps:
1. Understand the Components:
- Let E be the emf of the cell.
- Let r be the internal resistance of the cell.
- Let I be the current flowing through the circuit.
2. Apply Kirchhoff's Voltage Law (KVL):
- According to KVL, the sum of the potential differences in a closed loop is equal to zero.
- When traversing the loop, we consider the voltage drop across the internal resistance and the emf of the cell.
3. Set Up the Equation:
- As we move through the circuit, we encounter a voltage drop across the internal resistance r which is I⋅r.
- The emf E is considered positive when moving from the negative terminal to the positive terminal of the cell.
- Therefore, we can write the KVL equation as:
−I⋅r+E=0
4. Rearranging the Equation:
- Rearranging the above equation gives:
E=I⋅r+V
- Here, V is the terminal voltage across the external circuit.
5. Express Terminal Voltage:
- Rearranging the equation to express V in terms of E, I, and r:
V=E−I⋅r
Final Relation:
Thus, the relation between terminal voltage V, emf E, current I, and internal resistance r is given by:
V=E−I⋅r
- Let E be the emf of the cell.
- Let r be the internal resistance of the cell.
- Let I be the current flowing through the circuit.
- According to KVL, the sum of the potential differences in a closed loop is equal to zero.
- When traversing the loop, we consider the voltage drop across the internal resistance and the emf of the cell.
- As we move through the circuit, we encounter a voltage drop across the internal resistance r which is I⋅r.
- The emf E is considered positive when moving from the negative terminal to the positive terminal of the cell.
- Therefore, we can write the KVL equation as:
−I⋅r+E=0
- Rearranging the above equation gives:
E=I⋅r+V
- Here, V is the terminal voltage across the external circuit.
- Rearranging the equation to express V in terms of E, I, and r:
V=E−I⋅r
Thus, the relation between terminal voltage V, emf E, current I, and internal resistance r is given by:
V=E−I⋅r
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET - III (Delhi Board)
6 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET-II
33 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET - I
26 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
A cell of emf ε and internal resistance r is charged by a current I, then
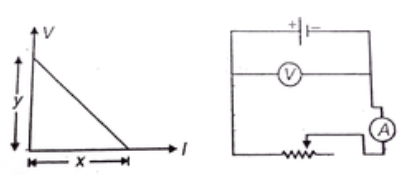
View SolutionFor the determination of emf E and internal resistance 'r' of a cell , the graph is obtained between potential difference V between the terminal of the cell against the current l, which was changed by adjusting the rheostat, is as shown . The internal resistance of the cell is
View SolutionA cell of emf ε and internal resistance r drives a current i through an extermal resistance R
(i) The cell suppllied εi power
(ii) Heat is produced in R at the rate εi
(iii) Heat is produced in R at the rate εI(RR+r)
(iv) Heat is produced in the cell at the rate εi(rR+r)
View SolutionA group of six identical cells each of emf E and internal resistance r are joined in series to form a loop. The terminal voltage across each cells is
View SolutionA cell of e.m. E and internal resistance r is connected across a resistancer. The potential difference between the terminals of the cell must be
View SolutionA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
View SolutionA cell of e.m.f. E and internal resistance r is used to send current to an external resistance R. Write expressions for (a) the total resistance of circuit, (b) the current drawn from the cell, (c) the p.d. across the cell, and (d) voltage drop inside the cell.
View SolutionA cell of e.m.f. 'E' and internal resistance 'r' is connected across a variable resistor 'R'. Plot a graph showing the variation of terminal potential 'V' with resistance R.
Predict from the graph the condition under which 'V' becomes equal of 'E'

View Solutionn' cells , each of emf 'e' and internal resistance 'r' are connected in a closed circuit so that the positive terminal of a cell is joined to the negative terminal of the next, as shown in figure. Any two points of the circuit are connected by an external resistance R. Find the current in R.
View SolutionA cell of emf E having an internal resistance R varies with R as shown in figure by the curve

View Solution
