An air cored solenoid is of length 0.3 m, area of cross section and has 2500 turns. Around its central section, a coil of 350 turns is wound. The solenoid and the coil are electrically insulated from eachother. Calculate the e.m.f. induced in the coil if the initial current of 3 A in the solenoid is reversed in 0.25 s.
To solve the problem step by step, we will calculate the induced electromotive force (e.m.f.) in the coil wound around the solenoid when the current in the solenoid is reversed.
Step 1: Identify the given values
- Length of the solenoid, L=0.3m
- Area of cross-section, A=1.2×10−3m2
- Number of turns in the solenoid, N1=2500
- Number of turns in the coil, N2=350
- Initial current, I1=3A
- Final current after reversal, I2=−3A
- Time taken for reversal, Δt=0.25s
Step 2: Calculate the change in current
The change in current, ΔI, is given by:
ΔI=I2−I1=−3A−3A=−6A
Step 3: Calculate the rate of change of current
The rate of change of current, dIdt, is calculated as:
dIdt=ΔIΔt=−6A0.25s=−24A/s
Step 4: Calculate the mutual inductance M
The mutual inductance M between the solenoid and the coil is given by the formula:
M=μ0N1N2AL
where μ0=4π×10−7T m/A.
Substituting the values:
M=4π×10−7×2500×350×1.2×10−30.3
Calculating the numerator:
2500×350×1.2×10−3=1050m2
Now substituting back:
M=4π×10−7×10500.3
M=4π×10−7×3500
M≈4×3.14×10−7×3500≈4.4×10−3H
Step 5: Calculate the induced e.m.f. E
The induced e.m.f. E in the coil can be calculated using:
E=−MdIdt
Substituting the values:
E=−4.4×10−3×(−24)=0.1056V
Final Answer
The induced e.m.f. in the coil is approximately:
E≈0.106V
- Length of the solenoid, L=0.3m
- Area of cross-section, A=1.2×10−3m2
- Number of turns in the solenoid, N1=2500
- Number of turns in the coil, N2=350
- Initial current, I1=3A
- Final current after reversal, I2=−3A
- Time taken for reversal, Δt=0.25s
The change in current, ΔI, is given by:
ΔI=I2−I1=−3A−3A=−6A
The rate of change of current, dIdt, is calculated as:
dIdt=ΔIΔt=−6A0.25s=−24A/s
The mutual inductance M between the solenoid and the coil is given by the formula:
M=μ0N1N2AL
where μ0=4π×10−7T m/A.
M=4π×10−7×2500×350×1.2×10−30.3
2500×350×1.2×10−3=1050m2
M=4π×10−7×10500.3
M=4π×10−7×3500
M≈4×3.14×10−7×3500≈4.4×10−3H
The induced e.m.f. E in the coil can be calculated using:
E=−MdIdt
Substituting the values:
E=−4.4×10−3×(−24)=0.1056V
The induced e.m.f. in the coil is approximately:
E≈0.106V
Topper's Solved these Questions
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:SET I
Explore 54 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:SET II
Explore 8 Videos
- SAMPLE PAPER 2019Book:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:SAMPLE PAPER 2019Exercise:SECTION D
Explore 6 Videos
Similar Questions
A solenoid is of length 50 cm and has a radius of 2cm. It has 500 turns. Around its central section a coil of 50 turns is wound. Calculate the mutual inductance of the system.
View SolutionA solenoid of 2000 turns is wound over a length of 0.3 m. The area aof cross section is 1.3×10−3m2. Around its central seciton, a coil of 300 turns is closely wound. If an initial current of 2 A is reversed in 0.25 s, find the e.m.f induced in the coil .
View Solution
Knowledge Check
A closely wound solenoid of 750 turns and area of cross section of 5×104m2 carries a current of 3.0 A. Its associated magnetic moment is
A4.12JT−1B3.12JT−1C2.12JT−1D1.13JT−1
A solenoidal coil has 50 turns per centimetre along its length and a cross-sectional area of 4×10−4m2. 200 turns of another wire is wound round the first solenoid co-axially. The two coils are electrically insulated from each other. Calculate the mutual inductance between the two coils.
View SolutionAn air cored solenoid of length 50 cm and area of cross section 28m2 has 200 turns and carries a current of 5.0 A. On switching off, the current decreases to across the ends of the solenoid. Find flux and emf induced if time is equal to 1.0 ms.
View SolutionA solenoid of length 20cm, area of cross- section 4.0cm2 and having 4000 turns is placed inside another solenoid of 2000 turns having a cross - sectional area 8.0cm2 and length 10cm. Find the mutual inductance between the solenoids.
View SolutionAn ideal solenoid of cross-sectional area 10−4m2 has 500 turns per metre. At the centre of this solenoid, another coil of 100 turns is wrapped closely around it. If the current in the coil changes from 0 to 2 A in 3.14 ms, the emf developed in the second coil is
View SolutionA long solenoid of length L, cross section A having N1 turns has about its center a small coil of N2 turns as shows in Fig The mutual inductance of two circuits is
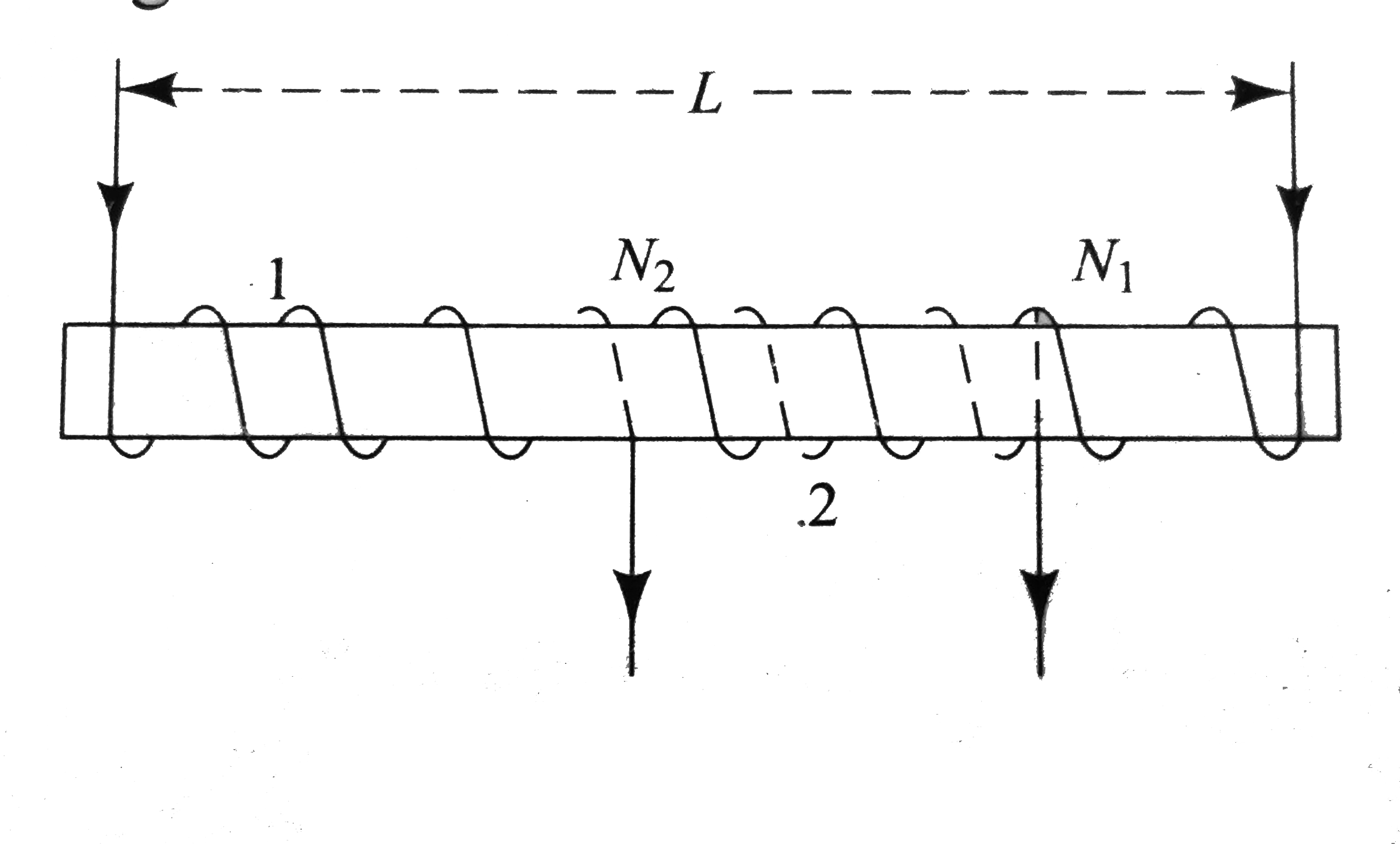
View SolutionA solenoid has 2000 turns would over a length of 0.30 m. The area of its cross-section is 1.2×10−3m2. If an initial current of 2 A in the solenoid is reversed in 0.25 s, then the emf induced in the coil is
View SolutionFor a toroid N = 500, radius = 40 cm, and area of cross section =10cm2. Find inductance
View Solution

