A solenoid of length 20cm, area of cross- section 4.0cm2 and having 4000 turns is placed inside another solenoid of 2000 turns having a cross - sectional area 8.0cm2 and length 10cm. Find the mutual inductance between the solenoids.
To find the mutual inductance between two solenoids, we can follow these steps:
Step 1: Identify the parameters of the solenoids
- Inner solenoid (S1):
- Length (l1) = 20 cm = 0.2 m
- Cross-sectional area (A1) = 4.0 cm² = 4.0 × 10⁻⁴ m²
- Number of turns (N1) = 4000 turns
- Outer solenoid (S2):
- Length (l2) = 10 cm = 0.1 m
- Cross-sectional area (A2) = 8.0 cm² = 8.0 × 10⁻⁴ m²
- Number of turns (N2) = 2000 turns
Step 2: Calculate the number of turns per unit length for both solenoids
- For the inner solenoid (S1):
n1=N1l1=40000.2=20000turns/m
- For the outer solenoid (S2):
n2=N2l2=20000.1=20000turns/m
Step 3: Calculate the magnetic field produced by the outer solenoid (S2)
The magnetic field (B2) inside the outer solenoid due to a current (I) flowing through it is given by:
B2=μ0⋅n2⋅I
Where μ0 (the permeability of free space) is approximately 4π×10−7H/m.
Step 4: Calculate the magnetic flux linked with the inner solenoid (S1)
The magnetic flux (Φ) linked with the inner solenoid is given by:
Φ=N1⋅B2⋅A1
Substituting for B2:
Φ=N1⋅(μ0⋅n2⋅I)⋅A1
Step 5: Calculate the induced EMF (E) in the inner solenoid (S1)
The induced EMF (E) is given by Faraday's law of electromagnetic induction:
E=−dΦdt
Substituting for Φ:
E=−ddt(N1⋅μ0⋅n2⋅I⋅A1)
This can be simplified to:
E=−M⋅dIdt
Where M is the mutual inductance.
Step 6: Express the mutual inductance (M)
From the equation above:
M=N1⋅μ0⋅n2⋅A1
Step 7: Substitute the values to calculate M
Substituting the known values:
- N1=4000
- μ0=4π×10−7H/m
- n2=20000turns/m
- A1=4×10−4m2
Calculating M:
M=4000⋅(4π×10−7)⋅20000⋅(4×10−4)
M=4000⋅4π⋅20000⋅4×10−11
M=64π×10−3H
Step 8: Calculate the numerical value of M
Using π≈3.14:
M≈64⋅3.14×10−3≈0.2H
Final Answer
The mutual inductance M between the two solenoids is approximately 0.2H.
---
- Inner solenoid (S1):
- Length (l1) = 20 cm = 0.2 m
- Cross-sectional area (A1) = 4.0 cm² = 4.0 × 10⁻⁴ m²
- Number of turns (N1) = 4000 turns
- Outer solenoid (S2):
- Length (l2) = 10 cm = 0.1 m
- Cross-sectional area (A2) = 8.0 cm² = 8.0 × 10⁻⁴ m²
- Number of turns (N2) = 2000 turns
- For the inner solenoid (S1):
n1=N1l1=40000.2=20000turns/m
n2=N2l2=20000.1=20000turns/m
The magnetic field (B2) inside the outer solenoid due to a current (I) flowing through it is given by:
B2=μ0⋅n2⋅I
Where μ0 (the permeability of free space) is approximately 4π×10−7H/m.
The magnetic flux (Φ) linked with the inner solenoid is given by:
Φ=N1⋅B2⋅A1
Substituting for B2:
Φ=N1⋅(μ0⋅n2⋅I)⋅A1
The induced EMF (E) is given by Faraday's law of electromagnetic induction:
E=−dΦdt
Substituting for Φ:
E=−ddt(N1⋅μ0⋅n2⋅I⋅A1)
This can be simplified to:
E=−M⋅dIdt
Where M is the mutual inductance.
From the equation above:
M=N1⋅μ0⋅n2⋅A1
Substituting the known values:
- N1=4000
- μ0=4π×10−7H/m
- n2=20000turns/m
- A1=4×10−4m2
M=4000⋅(4π×10−7)⋅20000⋅(4×10−4)
M=4000⋅4π⋅20000⋅4×10−11
M=64π×10−3H
Using π≈3.14:
M≈64⋅3.14×10−3≈0.2H
The mutual inductance M between the two solenoids is approximately 0.2H.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 2
10 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
7 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
8 Videos
Similar Questions
The self inductance of a solenoid of length L, area of cross-section A and having N turns is-
View SolutionA short solenoid of length 4 cm, radius 2 cm and 100 turns is placed inside and on the axis of a long solenoid of length 80 cm and 1500 turns. A current of 3 A flows through the short solenoid. The mutual inductance of two solenoid is
View Solution
Knowledge Check
The self inductance of a solenoid that has a cross-sectional area of 1cm2, a length of 10 cm and 1000 turns of wire is
A0.86mHB1.06mHC1.26mHD1.46mHA solenoid of lenght 30 cm with 10 turns per centimetre and area of cross-section 40cm2 completely surrounds another co-axial solenoid of same length, area of cross-section 20cm2 with 40 turns per centimetre. The mutual inductance of the system is
A10 HB8 HC3 mHD30 mH
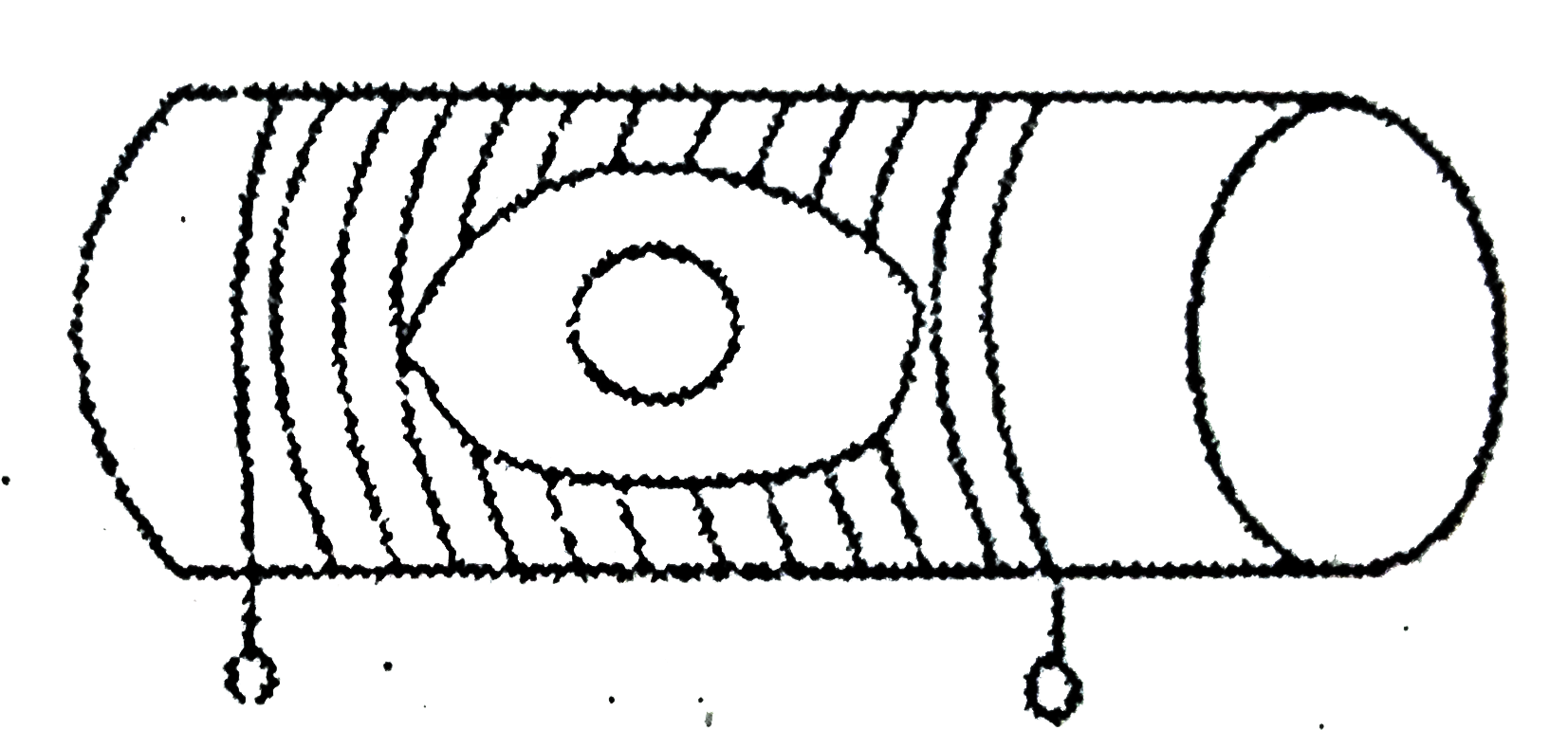
A circular coil with a cross-sectional area of 4cm2 has 10 turns. It is placed at the center of a long solenoid that has 15 turns/cm and a cross sectional area of 10cm2, shown in the figure. The axis of the coil conicides with the axis of the solenoid. What is their mutual inductance?
View SolutionAn air cored solenoid is of length 0.3 m, area of cross section 1.2×10−3m2 and has 2500 turns. Around its central section, a coil of 350 turns is wound. The solenoid and the coil are electrically insulated from eachother. Calculate the e.m.f. induced in the coil if the initial current of 3 A in the solenoid is reversed in 0.25 s.
View SolutionA solenoid of length 50cm with 20 turns per centimetre and area of cross-section 40cm? completely surrounds another coaxial solenoid of the same length, area of cross-section 25cm2 with 25 turns per centimetre. Calculate the mutual inductance of the system.
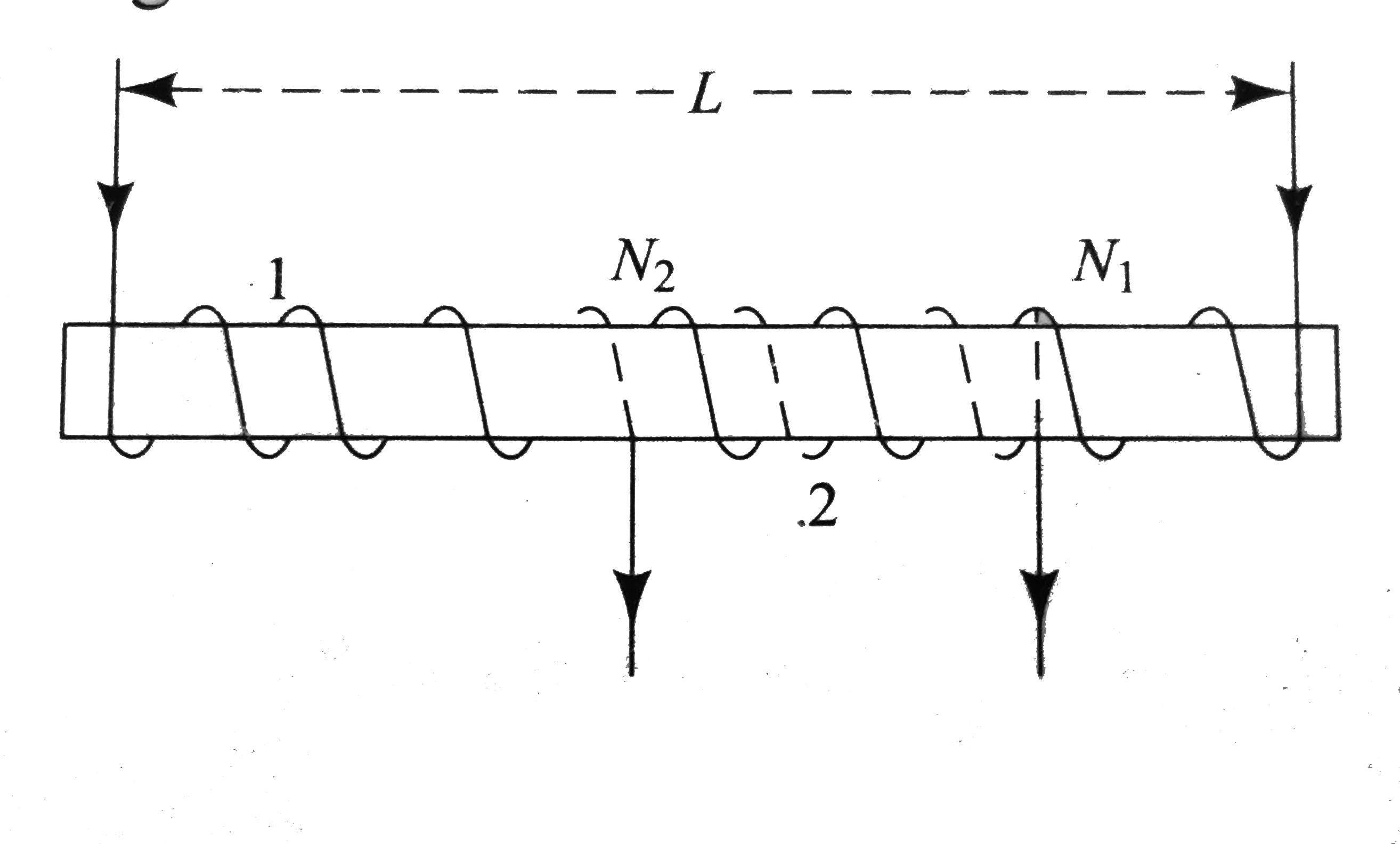
View SolutionA long solenoid of length L, cross section A having N1 turns has about its center a small coil of N2 turns as shows in Fig The mutual inductance of two circuits is
View SolutionA solenoid of radius 2.50cm has 400turns and a length of 20.0cm. The inductance (L) of this solenoid is ________.
View SolutionAn air cored solenoid of length 50 cm and area of cross section 28m2 has 200 turns and carries a current of 5.0 A. On switching off, the current decreases to across the ends of the solenoid. Find flux and emf induced if time is equal to 1.0 ms.
View Solution
