A beam of light converges at a point P. Now a convex lens is placed in the part of the converngent beam at 15 cm from P. At what point does a beam converge if the convex lens has a focad length 10 cm ?
To solve the problem step by step, we will use the lens formula:
1f=1v−1u
Where:
- f is the focal length of the lens,
- v is the image distance from the lens,
- u is the object distance from the lens.
Step 1: Identify the given values
- Focal length of the convex lens, f=10cm
- Distance from the point P to the lens, u=−15cm (the object distance is taken as negative in lens formula convention since the object is on the same side as the incoming light).
Step 2: Substitute the values into the lens formula
Using the lens formula:
1f=1v−1u
Substituting the values we have:
110=1v−1(−15)
Step 3: Rearranging the equation
Rearranging the equation to isolate 1v:
1v=110+115
Step 4: Finding a common denominator
To add the fractions, we need a common denominator. The least common multiple of 10 and 15 is 30.
110=330,115=230
So,
1v=330+230=530
Step 5: Solve for v
Now, we can find v:
1v=530⟹v=305=6cm
Step 6: Conclusion
The distance of the convergent point from the lens is 6cm.
---
- f is the focal length of the lens,
- v is the image distance from the lens,
- u is the object distance from the lens.
- Focal length of the convex lens, f=10cm
- Distance from the point P to the lens, u=−15cm (the object distance is taken as negative in lens formula convention since the object is on the same side as the incoming light).
Using the lens formula:
Rearranging the equation to isolate 1v:
To add the fractions, we need a common denominator. The least common multiple of 10 and 15 is 30.
Now, we can find v:
The distance of the convergent point from the lens is 6cm.
Topper's Solved these Questions
Similar Questions
A beam of light converges to a point P.A lens is placed in the path of the convergent beam 12cm from P. At what point does the beam converge if the lens is
(a) a convex lens of focal length 20cm. (b) a concave lens of focal length 16cm ?
View SolutionA beam of light converges to a point P. A lens is placed in the path of the covergent beam 12cm from P. At what point does the beam converge if the lens is
(a) a convex lens of focal length 20cm
(b) a concave lens of focal length 16cm ?
View SolutionA beam of light converges to a point on a screen S. A mirror is placed in front of the screen at a distance of 10cm form the screen. It is found that the beam now converges at a point 20cm in front of the mirror. Find the focal length of the mirror.
View SolutionFigure given below shows a beam of light converging at point P. When a concave lens of focal length 16cm is introduced in the path of the beam at a place O shown by dotted line such that OP becomes the axis of the lens, the beam converges at a distance x from the lens. The value x will be equal to
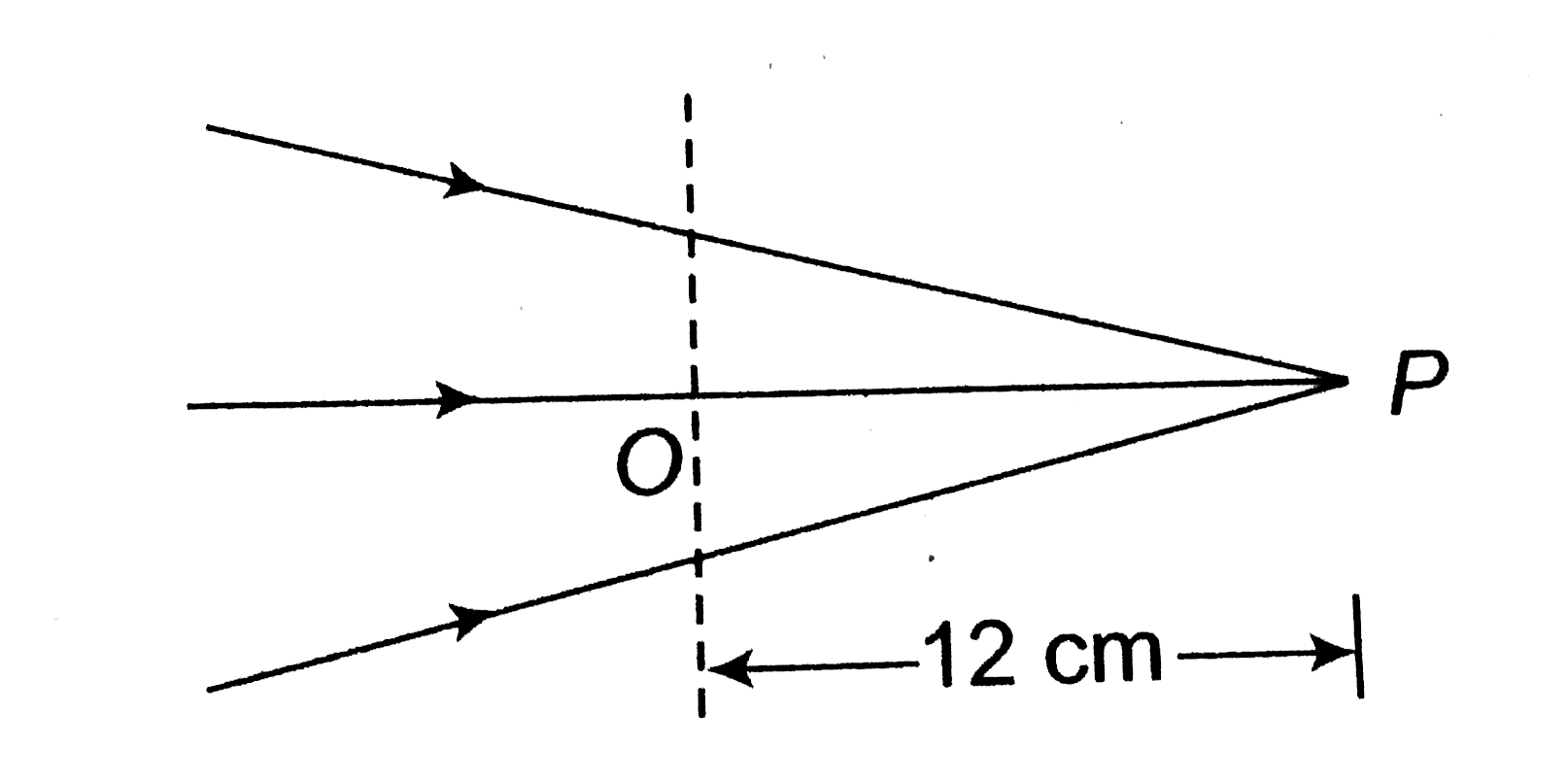
View SolutionA beam of light converges at a point P. Draw ray diagram to show where the beam will converge if (i) a convex lens and (ii) a concave lens is kept in the path of the beam?
View SolutionTwo thin lenses are placed 5cm apart along the same axis and illuminted with a beam of light parallel to that axis. The first lens in the path of the beam is a converging lens of focal length 10cm whereas the second is a diverging lens of focal length 5cm. If the second lens if now moved toward the first, the emergent light
View SolutionA converging beam of light is incident on a concave lens. The beam converges behind the lens at 15 cm from its centre, in the absence of the lens. Select the correct alternative
View SolutionA child has near point at 10 cm. What is the maximum angular magnification the child can have with a convex lens of focal length 10 cm?
View SolutionA beam of light converges towards a point O, behind a convex mirror of focal length 20cm.
Q. Find the magnification and nature of the image when point O is 10cm behind the mirror.
View SolutionA beam of light converges towards a point O, behind a convex mirror of focal length 20cm.
Q. Similarly, as in above question when point O is 30cm behind the mirror.
View Solution
