What is the minimum resistance which can be made using five resistors each of (1/5)Ω ?
1/5Ω
1/25Ω
1/10Ω
25Ω
The correct Answer is:B
To find the minimum resistance that can be achieved using five resistors, each with a resistance of 15Ω, we will connect them in parallel. Here’s the step-by-step solution:
Step 1: Understand the Configuration
To achieve the minimum resistance, we need to connect the resistors in parallel. When resistors are connected in parallel, the total or equivalent resistance decreases.
Step 2: Use the Formula for Parallel Resistance
The formula for the equivalent resistance Req of n resistors connected in parallel, each with resistance R, is given by:
Req=Rn
where R is the resistance of one resistor and n is the number of resistors.
Step 3: Substitute the Values
In this case, each resistor has a resistance of R=15Ω and we have n=5 resistors.
Req=155
Step 4: Simplify the Expression
Now, simplify the expression:
Req=15×15=125Ω
Step 5: Conclusion
Thus, the minimum resistance that can be achieved using five resistors of 15Ω each is:
Req=125Ω
Final Answer
The minimum resistance is 125Ω.
---
To achieve the minimum resistance, we need to connect the resistors in parallel. When resistors are connected in parallel, the total or equivalent resistance decreases.
The formula for the equivalent resistance Req of n resistors connected in parallel, each with resistance R, is given by:
Req=Rn
where R is the resistance of one resistor and n is the number of resistors.
In this case, each resistor has a resistance of R=15Ω and we have n=5 resistors.
Req=155
Now, simplify the expression:
Req=15×15=125Ω
Thus, the minimum resistance that can be achieved using five resistors of 15Ω each is:
Req=125Ω
The minimum resistance is 125Ω.
Topper's Solved these Questions
Similar Questions
What is the maximum resistance which can be made using five resistors each of (1/5)Ω ?
View Solution(a) Given n resistors each of resistance R. How will you combine them to get the (i) maximum (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
(b) Given the resistances of 1Ω,2Ω,3Ω, how will you combine them to get an equivalent resistance of (i) (11/3)Ω (ii) (11/5)Ω (iii) 6Ω (iv) (6/11)Ω ?
(c) Determine the equivalent resistance of networks shown in Figure.
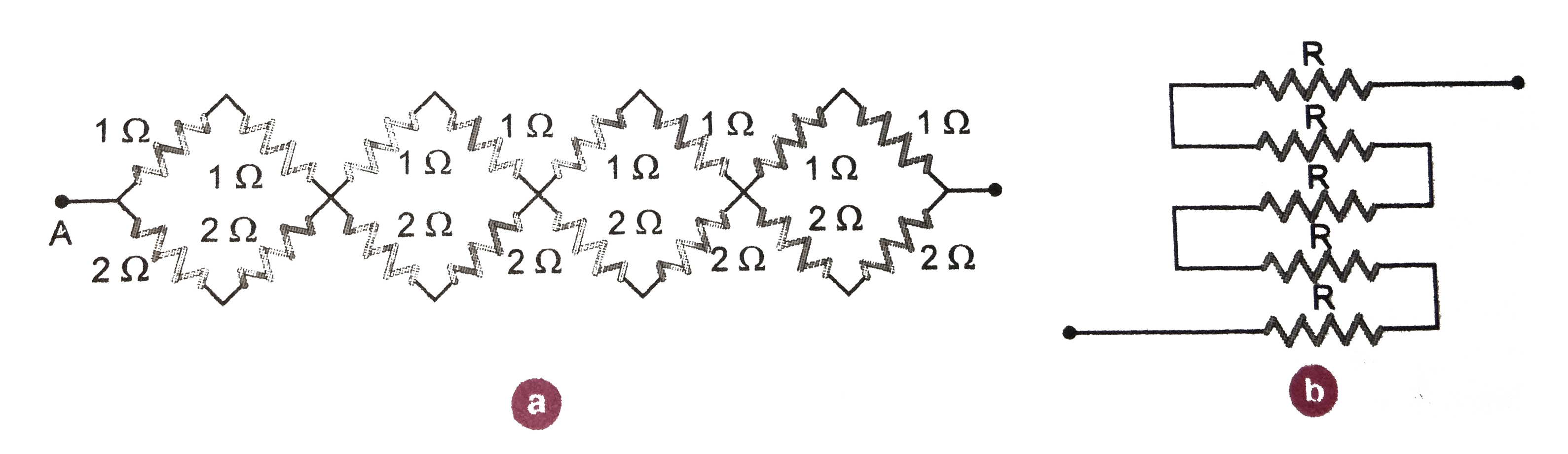
View SolutionIn the process of electroplating m gram of silver is deposited when 4 amp of current flows for 2 min The amount in (gm) of silver deposited by 6 amp of current flowing for 40 second will be
View SolutionWhat is the resistance between P and Q in the following circuit? Each resistance is of 1Ω and the wire between eb and bd have resistance 0.5Ω each.

View SolutionMinimum resistance obtained from two resistors 3Ω and 2Ω is
View SolutionIn the circuit shown in the figure , the resistance marked R can be varied by using a Rheostat. The power across the 5 Omega resistor will be maximum if the Rhoestat has resistance equal to
_PHY_E01_015_Q01.png)
View SolutionA cell of e.m.f. 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and a resistor of 4.5 Ω as shown in Fig.
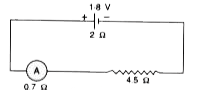
What would be the reading of the ammeter ?
View SolutionWhat is the smallest that can be obtained by ten 110Ω resistance.
View SolutionWhat are the maximum and minimum values of unknown resistance X, which can be determined using the post office box shown in the figure?
View SolutionA cell of e.m.f. 2V and internal resistance 1.2.Ω is connected with an ammeter of resistance 0.8Ω and two resistors of 4.5 Ω and 9Ω as shown in the diagram below:
What would be the reading on the Ammeter?
View Solution
