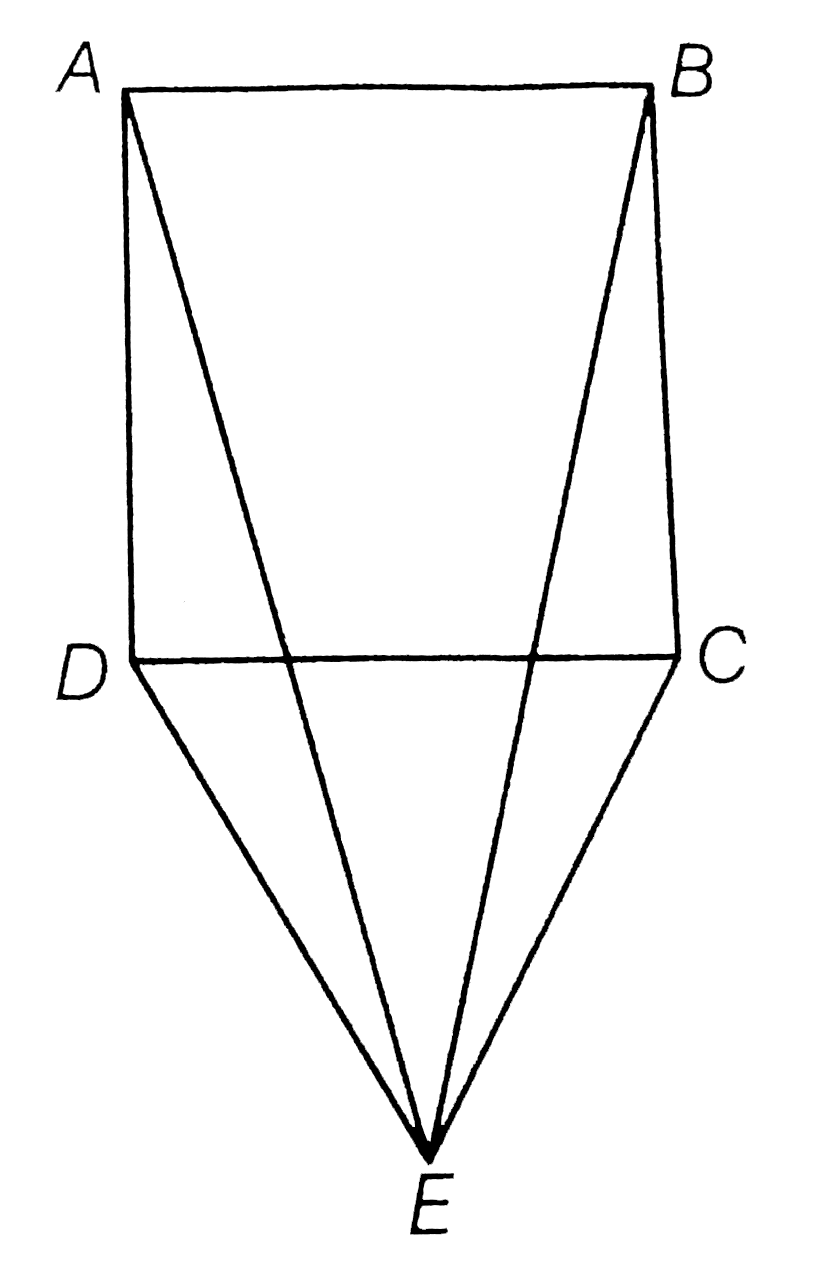
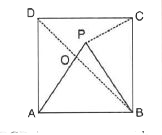
In the given figure, is an equilateral triangle triangle formed on a side of a square . Show that
Video Solution
Text Solution
Given in figure is an equilateral triangle formed on a side CD of a square ABCD.
To show
Proof in
|
Topper's Solved these Questions
- TRIANGLESBook:NCERT EXEMPLAR ENGLISHChapter:TRIANGLESExercise:LONG ANSWER TYPE QUESTIONS
Explore 21 Videos
- TRIANGLESBook:NCERT EXEMPLAR ENGLISHChapter:TRIANGLESExercise:VERY SHORT ANSWER TYPE QUESTIONS
Explore 12 Videos
- STATISTICS AND PROBABILITYBook:NCERT EXEMPLAR ENGLISHChapter:STATISTICS AND PROBABILITYExercise:LONG ANSWER TYPE QUESTIONS
Explore 12 Videos
- VOLUME AND SURFACE AREABook:NCERT EXEMPLAR ENGLISHChapter:VOLUME AND SURFACE AREAExercise:LONG ANSWER TYPE QUESTIONS
Explore 8 Videos
Similar Questions
Knowledge Check
Find the area of an equilateral triangle with a side length of 12
A6√3B18√3C36√3D72√3
In the given figure, ΔABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices.
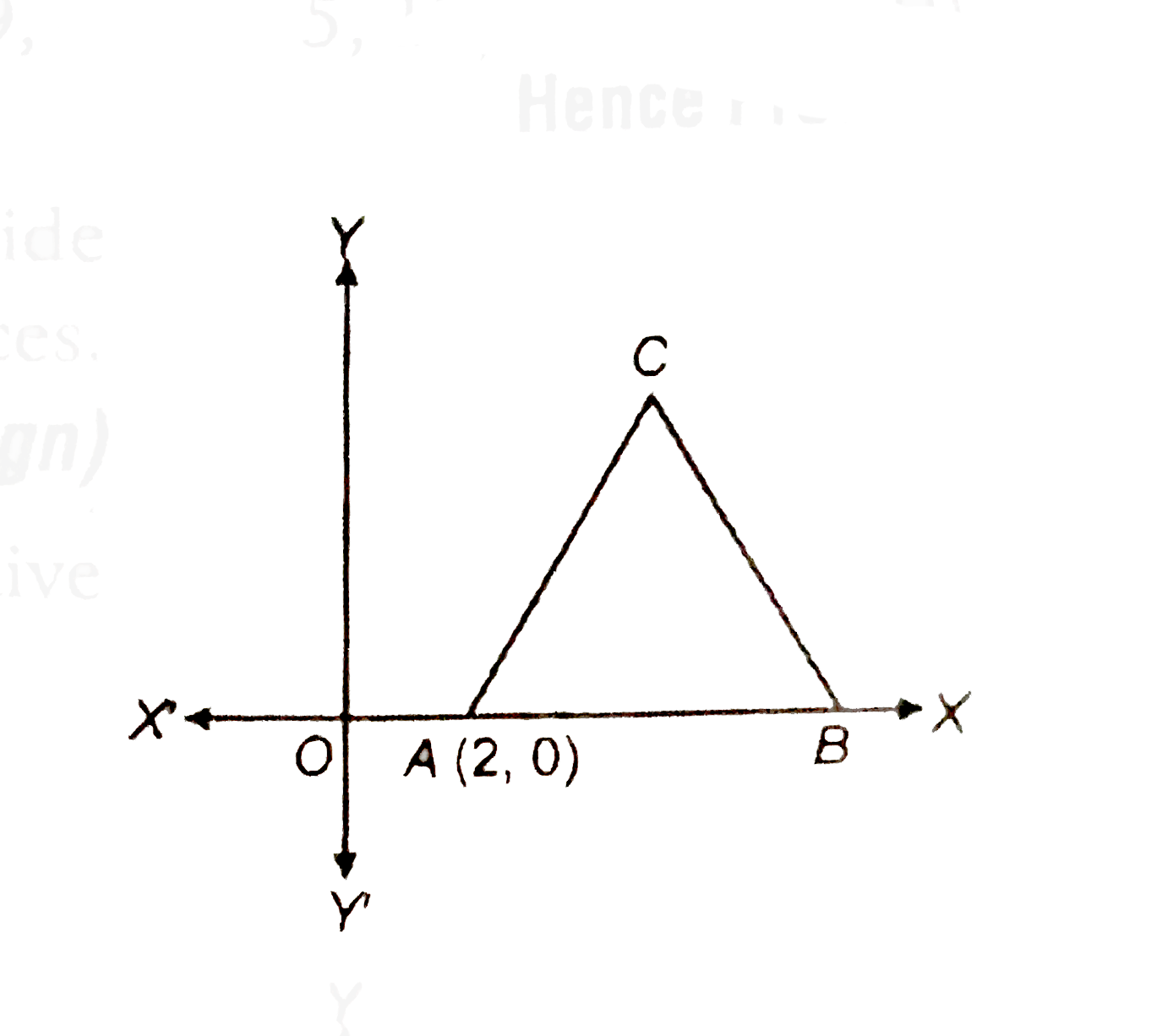
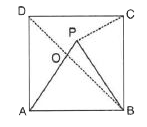
View SolutionThe given figure shows a square ABCD and an equilateral triangle ABP. Calculate:
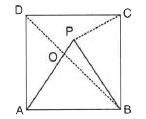
∠PCD
View SolutionThe given figure shows a square ABCD and an equilateral triangle ABP. Calculate:
∠BPC
View SolutionConstruct an equilateral triangle of sides 6 cm each.
View SolutionFind the perimeter of an equilateral triangle with side 9cm.
View SolutionFind the altitude of an equilateral triangle of side 8 cm.
View SolutionThe given figure shows a square ABCD and an equilateral triangle ABP. Calculate:
∠AOB
View Solution

