In figure ,D and E are Points on side BC of a ΔABC such that BD=CE and AD=AE. Show that ΔABD≅ΔACE.
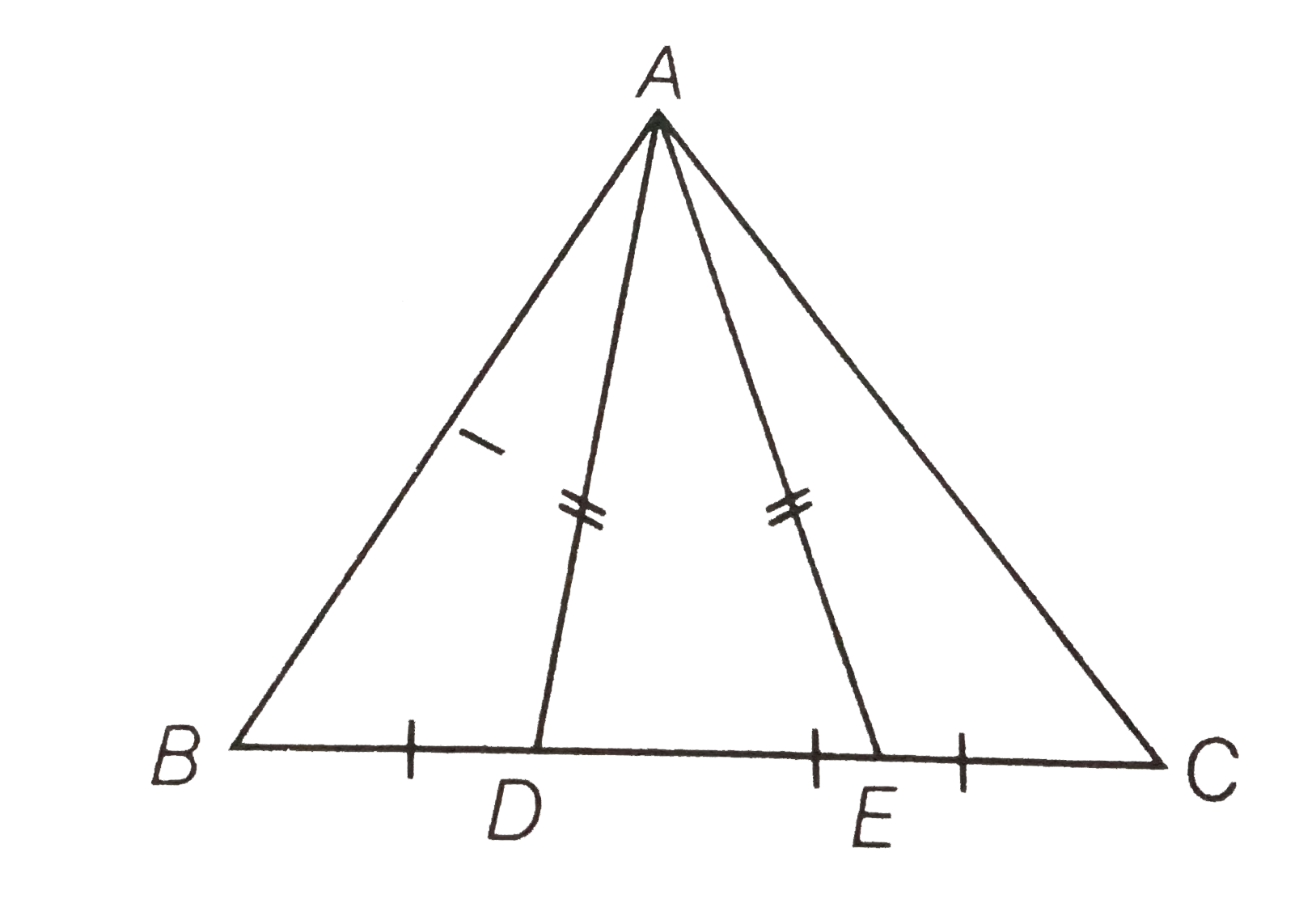
Given D and E are the point on side BC of a ΔABCSuch that BD =CE and AD=AE.
To show ΔABD≅ΔACE
Proof We have, AD=AE [given]
⇒ ∠ADE=∠AED …(i)
[since angle opposite to equal sides are equal ]
We have ∠ADB+∠ADE=180∘ [linear Pair axiom]
⇒ ∠ADB=180∘−∠AED
=180∘−∠AED [from Eq.(i)]
InΔABDandΔACE,
∠ADB=∠AEC [∵∠AEC+∠AED=180∘,Linear Pair axiom]
BD=CE [given]
∴ ΔABD≅ΔACE [by SAS congruence rule]
Topper's Solved these Questions
- TRIANGLESBook:NCERT EXEMPLAR ENGLISHChapter:TRIANGLESExercise:LONG ANSWER TYPE QUESTIONS
Explore 21 Videos
- TRIANGLESBook:NCERT EXEMPLAR ENGLISHChapter:TRIANGLESExercise:VERY SHORT ANSWER TYPE QUESTIONS
Explore 12 Videos
- STATISTICS AND PROBABILITYBook:NCERT EXEMPLAR ENGLISHChapter:STATISTICS AND PROBABILITYExercise:LONG ANSWER TYPE QUESTIONS
Explore 12 Videos
- VOLUME AND SURFACE AREABook:NCERT EXEMPLAR ENGLISHChapter:VOLUME AND SURFACE AREAExercise:LONG ANSWER TYPE QUESTIONS
Explore 8 Videos
Similar Questions
In the given figure, D and E are the points on the base BC of ΔABC such that BD=CE,AD=AE and ∠ADE=∠AED, prove that ΔADB≅ΔAEC.
View SolutionIf D is a Point on the side BC of a ΔABC such that AD bisects ∠BAC. Then
View SolutionIn figure ,BA⊥AC,DE⊥DF such that BA = DE and BF = EC. Show that ΔABC≅ΔDEF.
View SolutionD is any point on side AC of a ΔABC with AB= AC .Show that CD<BD.
View SolutionThe figure, given alongside, shows a trapezium ABCD in which AB/DC and AD= BC. Prove that:
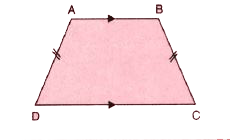
ΔABC≅ΔBAD
View SolutionIn the adjoning figure, D and E are the points on the sides AB and AC respectively of ΔABC and area of ΔBCE= area of ΔBCD.
Prove that DE∣∣BC
View SolutionD is a point in side BC of triangle ABC. If AD>AC, show that AB>AC.
View SolutionAny point D is taken on the side BC of a ΔABC and AD is produced to E such that AD = DE , prove that area of ΔBCE= area of ΔABC,
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View Solution

