AD is a median of the ΔABC.Is it trure AB+BC+CA>2AD? Give reason for your answer
Yes
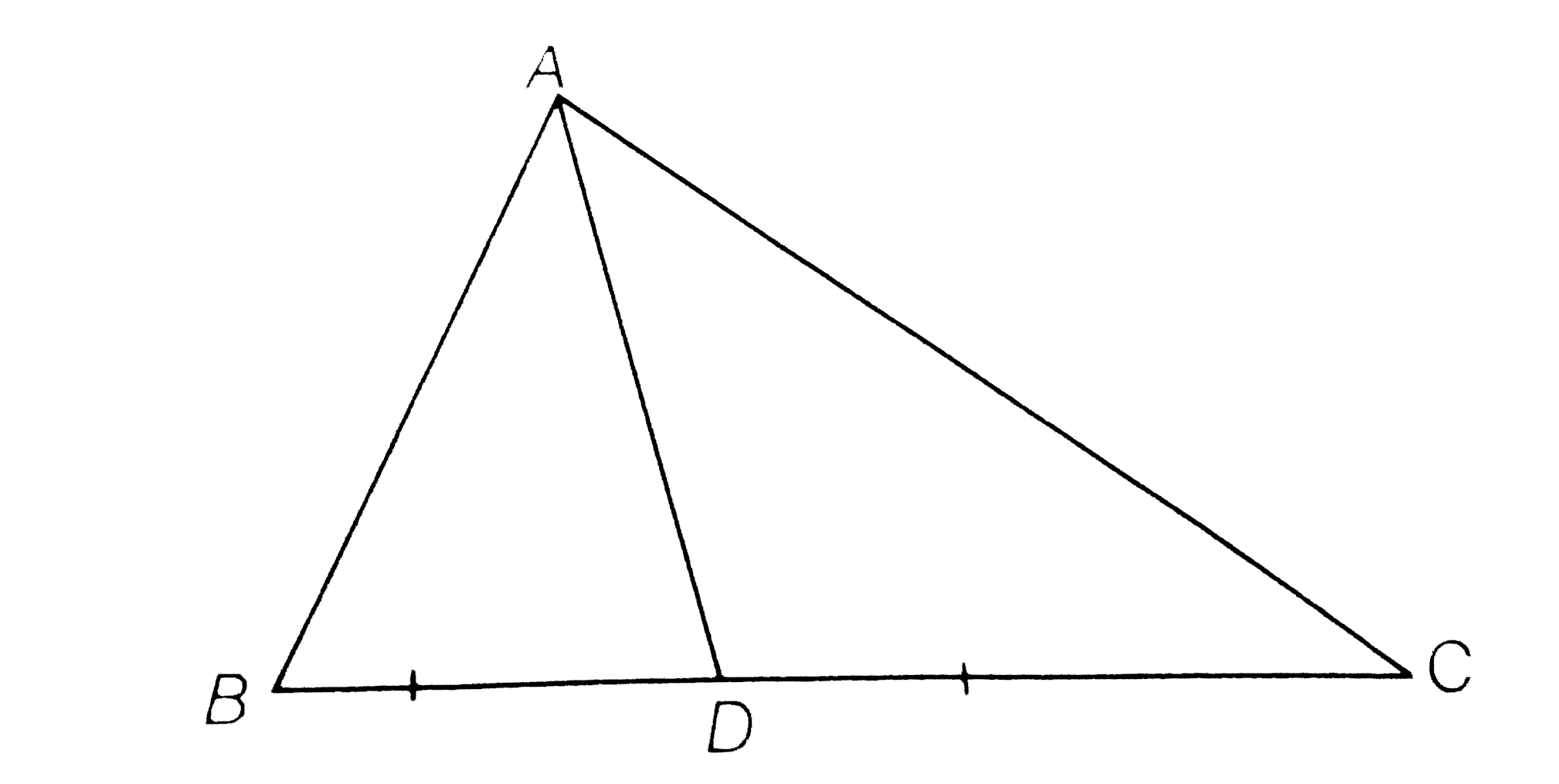
In ΔABD,wehave AB+BD>AD
[Sum of any two sides of a triangle is great than third side]
In ΔACD,Wehave AC+CD>AD
[Sum of any two sides of a triangle is greater than third side]
On adding Eqs.(i) and (ii) we get
(AB+BD+CD+AC)>2AD
⇒ (AB+BD+CD+AC)>2AD
Hence AB+BC+AC>2AD [∵BC=BD+CD]
Topper's Solved these Questions
- TRIANGLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - SHORT ANSWER TYPE QUESTIONS
11 Videos
- TRIANGLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - LONG ANSWER TYPE QUESTIONS
21 Videos
- TRIANGLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - LONG ANSWER TYPE QUESTIONS
21 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS
12 Videos
- VOLUME AND SURFACE AREABOOK - NCERT EXEMPLAR ENGLISHCHAPTER - VOLUME AND SURFACE AREAEXERCISE - LONG ANSWER TYPE QUESTIONS
8 Videos
Similar Questions
AD is a median of triangle ABC. Prove that : AB+BC+AC>2AD
View SolutionM is point on side BC of a triangle ΔABC such that AM is the bisector of ∠BAC. Is it true to say that perimeter of the triangle is greater than 2 AM ? Give reason for your answer ?
View SolutionIn ΔABCandΔPQR,∠A=∠Qand∠B=∠R. Which side of ΔPQRshould be equal to side BC of ΔABC ,so that the two triangle are congruent ? Give reason for your answere.
View SolutionIn ΔABCandΔPQR,∠A=∠Qand∠B=∠R. Which side of ΔPQR should be equal to side AB of ΔABC, so that the two triangle are congruent ? Give reason for your answer.
View SolutionAD is a median of triangle ABC. Prove that : AB+AC>2AD
View SolutionAM is a median of s triangle ABC. Is AB+BC+CA>2AM? (Consider the sides of triangles ΔABMandΔAMC.
View SolutionLet AD be a median of the ΔABC. If AE and AF are medians of the triangle ABD and ADC, respectively, and BD=a/2 AD = m1,AE=m2,AF=m3, then a2/8 is equal to
View SolutionIn the given figure AD is the median. If the area of ΔABD=10cm2, find the area of ΔABC
View SolutionIf D is a Point on the side BC of a ΔABC such that AD bisects ∠BAC. Then
View SolutionIn the adjoining figure, AD is the median of ΔABC and X be any point on side AD. Prove that:
area (ΔABX)= area (ΔACX)

View Solution
