In ΔABCandΔPQR , If AB=AC, ∠C=∠P and ∠B=∠Q, then the two triangles are
isosceles but not congruent
isosceles and congruent
congruent but not isosceles
Neither congruent nor isosceles
The correct Answer is:A
To solve the problem, we need to analyze the given information about triangles ABC and PQR.
1. Identify Given Information:
- We have two triangles: ΔABC and ΔPQR.
- It is given that AB = AC (sides of triangle ABC are equal).
- It is also given that ∠C = ∠P and ∠B = ∠Q.
2. Determine the Type of Triangle ABC:
- Since AB = AC, by the property of isosceles triangles, we know that the angles opposite to equal sides are equal. Therefore, ∠B = ∠C.
- This means triangle ABC is an isosceles triangle because it has at least two equal sides (AB and AC).
3. Analyze the Angles:
- We know that ∠C = ∠P and ∠B = ∠Q.
- Since ∠B = ∠Q (from the given information), we can conclude that ∠C = ∠P = ∠Q.
4. Determine the Type of Triangle PQR:
- Since ∠C = ∠P and ∠B = ∠Q, we can say that triangle PQR also has two equal angles (∠P and ∠Q).
- Therefore, triangle PQR is also an isosceles triangle.
5. Conclusion:
- Both triangles ABC and PQR are isosceles triangles because they each have at least two equal sides and two equal angles.
- However, we cannot conclude that the triangles are congruent because they do not share all three pairs of equal sides or angles (AAA does not guarantee congruence).
Thus, the final answer is that the two triangles are isosceles.
- We have two triangles: ΔABC and ΔPQR.
- It is given that AB = AC (sides of triangle ABC are equal).
- It is also given that ∠C = ∠P and ∠B = ∠Q.
- Since AB = AC, by the property of isosceles triangles, we know that the angles opposite to equal sides are equal. Therefore, ∠B = ∠C.
- This means triangle ABC is an isosceles triangle because it has at least two equal sides (AB and AC).
- We know that ∠C = ∠P and ∠B = ∠Q.
- Since ∠B = ∠Q (from the given information), we can conclude that ∠C = ∠P = ∠Q.
- Since ∠C = ∠P and ∠B = ∠Q, we can say that triangle PQR also has two equal angles (∠P and ∠Q).
- Therefore, triangle PQR is also an isosceles triangle.
- Both triangles ABC and PQR are isosceles triangles because they each have at least two equal sides and two equal angles.
- However, we cannot conclude that the triangles are congruent because they do not share all three pairs of equal sides or angles (AAA does not guarantee congruence).
Topper's Solved these Questions
- TRIANGLESBook:NCERT EXEMPLAR ENGLISHChapter:TRIANGLESExercise:VERY SHORT ANSWER TYPE QUESTIONS
Explore 12 Videos
- TRIANGLESBook:NCERT EXEMPLAR ENGLISHChapter:TRIANGLESExercise:SHORT ANSWER TYPE QUESTIONS
Explore 11 Videos
- STATISTICS AND PROBABILITYBook:NCERT EXEMPLAR ENGLISHChapter:STATISTICS AND PROBABILITYExercise:LONG ANSWER TYPE QUESTIONS
Explore 12 Videos
- VOLUME AND SURFACE AREABook:NCERT EXEMPLAR ENGLISHChapter:VOLUME AND SURFACE AREAExercise:LONG ANSWER TYPE QUESTIONS
Explore 8 Videos
Similar Questions
In ΔABCandΔPQR,∠A=∠Qand∠B=∠R. Which side of ΔPQR should be equal to side AB of ΔABC, so that the two triangle are congruent ? Give reason for your answer.
View SolutionIn ΔABCandΔPQR,∠A=∠Qand∠B=∠R. Which side of ΔPQRshould be equal to side BC of ΔABC ,so that the two triangle are congruent ? Give reason for your answere.
View SolutionIn ΔABCandΔDEF, ∠B=∠E,∠F=∠C and AB=3DE. Then, the two triangles are
View SolutionIn ΔPQR, If angleR=angleP, QR=4 cm and PR = 5 cm. Then, the length of PQ is
View SolutionWhich of the following pairs of triangles are congruent ? In each case, state the condition of congruency :
(a) In ΔABCandΔDEF, AB = DE, BC = EF and ∠B=∠E.
(b) In ΔABCandΔDEF,∠B=∠E=90∘, AC = DF and BC = EF.
(c) In ΔABCandΔQRP, AB = QR, ∠B=∠Rand∠C=∠P.
(d) In ΔABCandΔPQR, AB = PQ, AC = PR and BC = QR.
(e) In ΔABCandΔPQR, BC = QR, ∠A=90∘,∠C=∠R=40∘and∠Q=50∘.
View SolutionIn ΔABC, if AB=AC and ∠B=50∘, then ∠C is equal to
View SolutionIn a ΔABC,∠A=2∠B=3∠C, find each of the triangle.
View SolutionIn ΔABC,∠A=x+15∘,∠B=xand∠C=2x−35∘ find, each angle of the triangle.
View SolutionABC is an isosceles triangle with AB=AC and D is a point on ABC BC such that AD⊥BC (see figure ). To prove that ∠BAD=∠CAD a student proceeded as follows
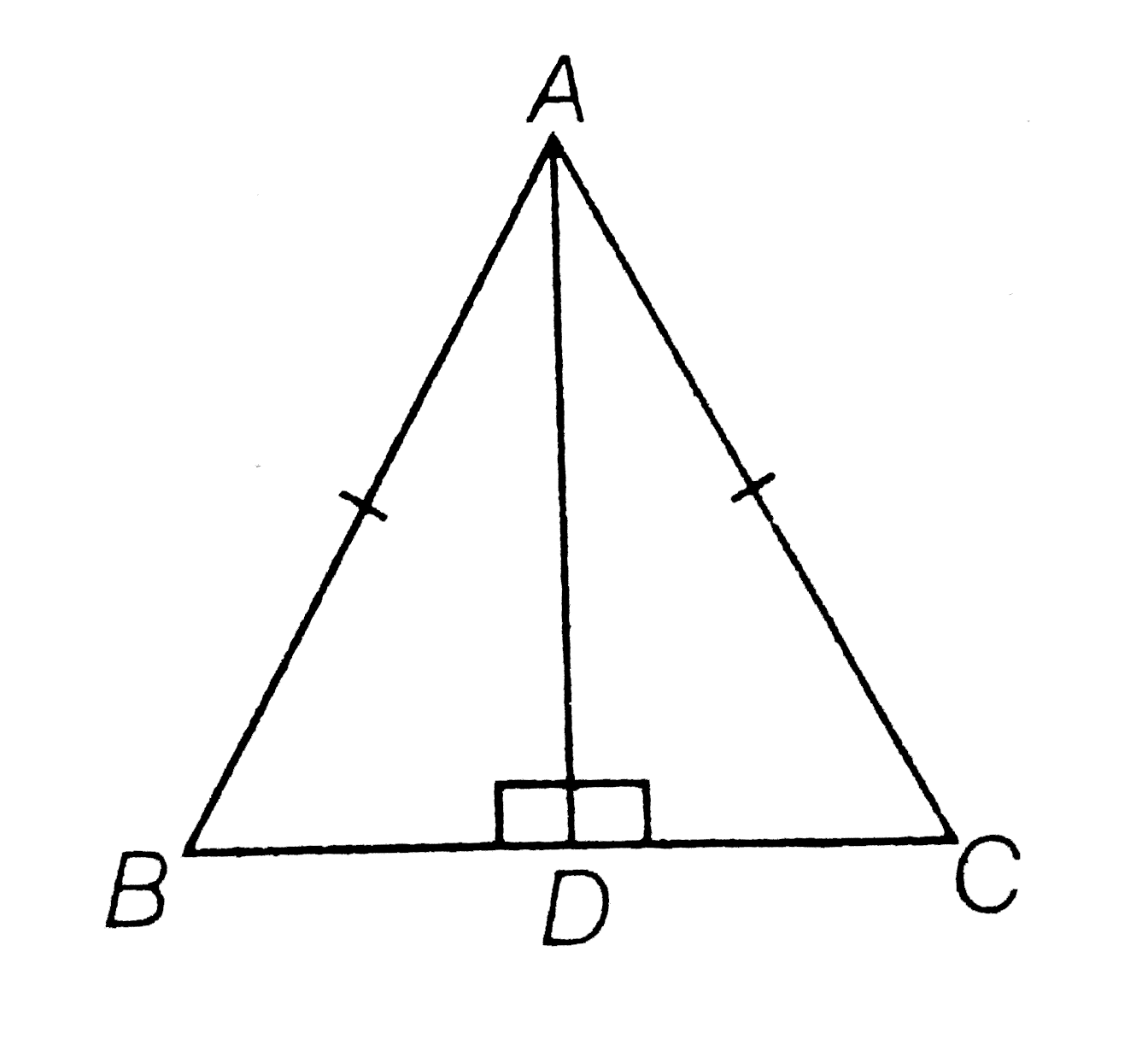
InΔABDandΔACD,we have
AB=AC [ Given]
∠B=∠C [∵ AB=AC ]
and ∠ADB=∠ADC
Therefore ΔABD≅ΔACD [by AAS congruence rule]
So , ∠BAD=∠CAD [byCPCT]
What is the defect in the above argument ?
View SolutionFind ∠A+∠B+∠C+∠P+∠Q+∠R.

View Solution