In figure BD and CE intersect each other at the point P. IsΔPBC~ΔPDE? Why?

True
In ΔPBCandΔPDE,
∠BPC=∠EPD [vertically opposite angle]
Now PBPD=510=12
and PCPE=612=12
From Eqs. (i) and (ii) PBPD=PCPE
Since. One angle of ΔPBC is equal to one angle of ΔPDE and the sides including these angles are proportional, so both triangles are similar.
Hence. ΔPBC~ΔPDE, by SAS similarity criterion.
Topper's Solved these Questions
- TRIANGLESBook:NCERT EXEMPLAR ENGLISHChapter:TRIANGLESExercise:Short Answer Type Questions
Explore 15 Videos
- TRIANGLESBook:NCERT EXEMPLAR ENGLISHChapter:TRIANGLESExercise:Long Answer Type Questions
Explore 18 Videos
- TRIANGLESBook:NCERT EXEMPLAR ENGLISHChapter:TRIANGLESExercise:Long Answer Type Questions
Explore 18 Videos
- SURFACE AREAS AND VOLUMESBook:NCERT EXEMPLAR ENGLISHChapter:SURFACE AREAS AND VOLUMESExercise:LONG ANSWER TYPE QUESTIONS
Explore 20 Videos
Similar Questions
In Figure, two chords AB and CD intersect each other at the point P. Prove that:
(i) ΔAPC~ΔDPB
(ii) AP⋅PB=CP⋅DP

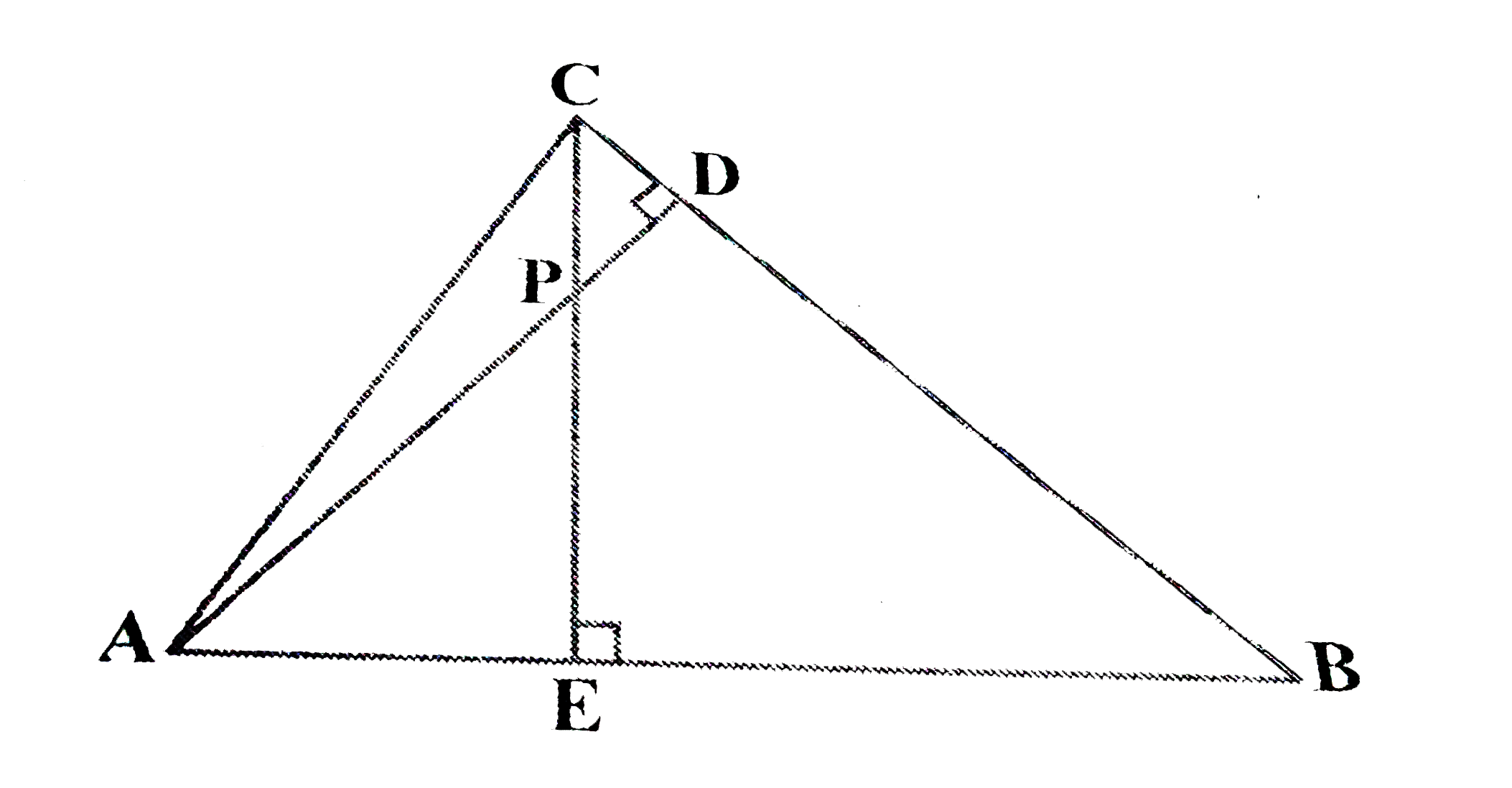
View SolutionIn Figure altitudes AD and CE of A B C intersect each other at the point P. Show that:(i) ΔAEP~ΔCDP (ii) ΔABD~ΔCBE (iii) ΔAEP~ΔADB(iv) ΔPDC~ΔBEC
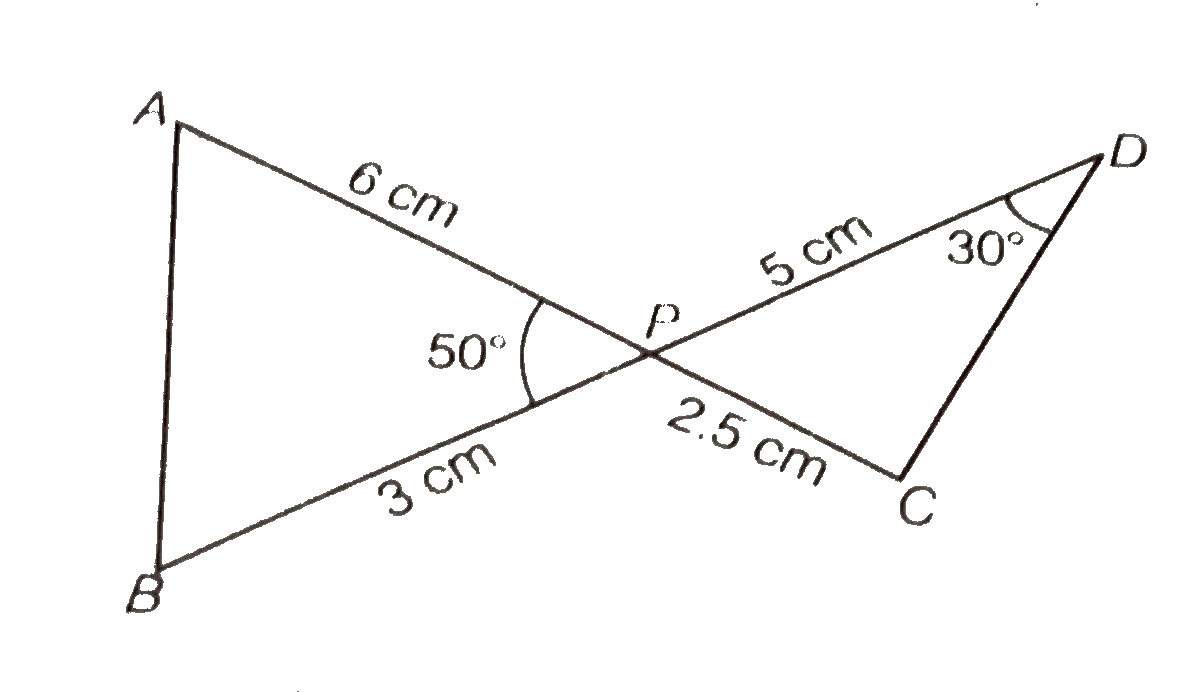
View SolutionIn figure, two line segments AC and BD intersects each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD=5 cm, ∠APB=50∘ and ∠CDP=30∘. Then, ∠PBA is equal to
View SolutionIn Figure two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC~ΔPDB
(ii) PA⋅PB = PC⋅PD

View SolutionIn parallelogram ABCD, P is mid-point of AB. CP and BD intersect each other at point O. If area of ΔPOB=40cm2 and OP:OC= 1:2, find :
(i) Areas of ΔBOC and ΔPBC
(ii) Areas of ΔABC and parallelogram ABCD.
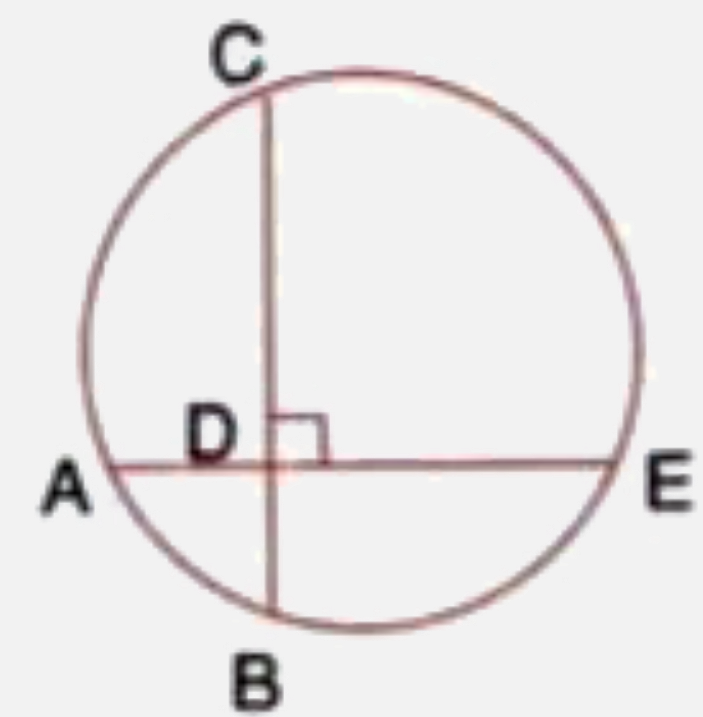
View SolutionIn the given figure, AE and BC intersect each other at point D.
If ∠CDE=90∘,AB=5cm,BD=4 and CD=9 find AE
View SolutionIn a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
ΔAPB is similar to ΔCPD.
View SolutionIn parallelogram ABCD, the bisectors of adjacent angles A and D intersect each other at point P. prove that ∠APD=90∘.
View SolutionIn a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
PA×PD=PB×PC.
View SolutionIn △ABC,E and F are mid-points od sides AB and AC respectively. If BF and CE intersect each other at point O, prove that the ΔOBC and quadrilateral AEOF are equal in area.
View Solution

