D is a point on side QR of ΔPQR such that PD⊥QR. Will it be correct to say that ΔPQD~ΔRPD? Why?
To determine whether triangle ΔPQD is similar to triangle ΔRPD, we will analyze the triangles based on the given information.
1. Identify the triangles: We have triangle PQR with point D on side QR such that PD is perpendicular to QR. This means that PD forms a right angle with QR.
2. List the triangles: The two triangles we are considering are ΔPQD and ΔRPD.
3. Identify common elements:
- Both triangles share the side PD. Therefore, we can say that PD=PD (common side).
4. Identify the right angles:
- Since PD is perpendicular to QR, we have:
- ∠PDQ=90∘ (right angle in triangle PQD)
- ∠PDR=90∘ (right angle in triangle RPD)
5. Compare angles:
- We have established that:
- PD=PD (common side)
- ∠PDQ=∠PDR=90∘ (both angles are right angles)
6. Check for similarity criteria:
- For two triangles to be similar, we typically look for criteria like AA (Angle-Angle), SSS (Side-Side-Side), or SAS (Side-Angle-Side).
- Here, we have one angle (the right angle) and one side that is common, but we do not have a second angle or sufficient information about the other sides.
7. Conclusion:
- Since we do not have enough information to satisfy any of the similarity criteria (specifically, we lack a second angle), we cannot conclude that ΔPQD∼ΔRPD.
- Therefore, it is incorrect to say that ΔPQD is similar to ΔRPD.
Final Answer:
No, it is not correct to say that ΔPQD∼ΔRPD because we do not have enough information to satisfy the criteria for similarity.
---
- Both triangles share the side PD. Therefore, we can say that PD=PD (common side).
- Since PD is perpendicular to QR, we have:
- ∠PDQ=90∘ (right angle in triangle PQD)
- ∠PDR=90∘ (right angle in triangle RPD)
- We have established that:
- PD=PD (common side)
- ∠PDQ=∠PDR=90∘ (both angles are right angles)
- For two triangles to be similar, we typically look for criteria like AA (Angle-Angle), SSS (Side-Side-Side), or SAS (Side-Angle-Side).
- Here, we have one angle (the right angle) and one side that is common, but we do not have a second angle or sufficient information about the other sides.
- Since we do not have enough information to satisfy any of the similarity criteria (specifically, we lack a second angle), we cannot conclude that ΔPQD∼ΔRPD.
- Therefore, it is incorrect to say that ΔPQD is similar to ΔRPD.
No, it is not correct to say that ΔPQD∼ΔRPD because we do not have enough information to satisfy the criteria for similarity.
Topper's Solved these Questions
- TRIANGLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Short Answer Type Questions
15 Videos
- TRIANGLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Long Answer Type Questions
18 Videos
- TRIANGLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Long Answer Type Questions
18 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS
20 Videos
Similar Questions
If S is a point on side PQ of a ΔPQR such that PS=QS=RS, then
View SolutionS is any point on side QR of a ΔPQR. Show that PQ+QR+RP>2PS .
View SolutionS and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS Show that ΔRPQ~ΔRTS
View SolutionS and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS. Show that ΔRPQ~ΔRTS.
View SolutionIf S is the mid-point of side QR of a ΔPQR, then prove that PQ+PR=2PS.
View SolutionPQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

area of ΔPQRarea of ΔSPR
View SolutionPQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

Find the lengths of QR and PS.
View SolutionPQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

Prove ΔPQR~ΔSPR.
View SolutionIn a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
ΔPQL~ΔRPM
View SolutionIn a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
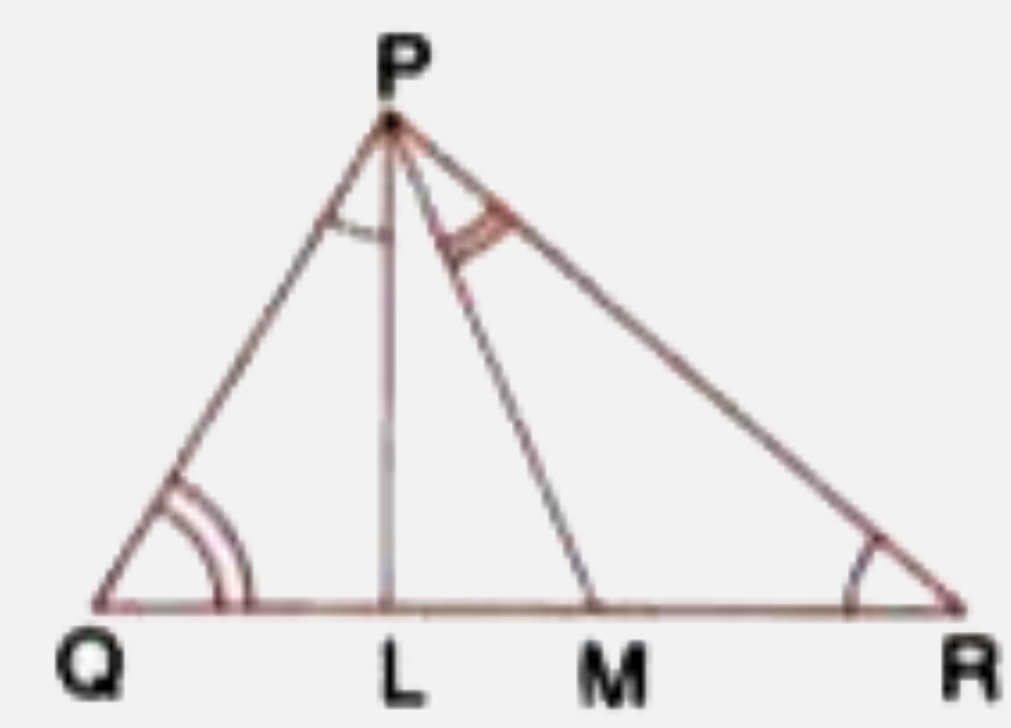
ΔPQL~ΔRPM
View Solution
