In figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD+∠BED.
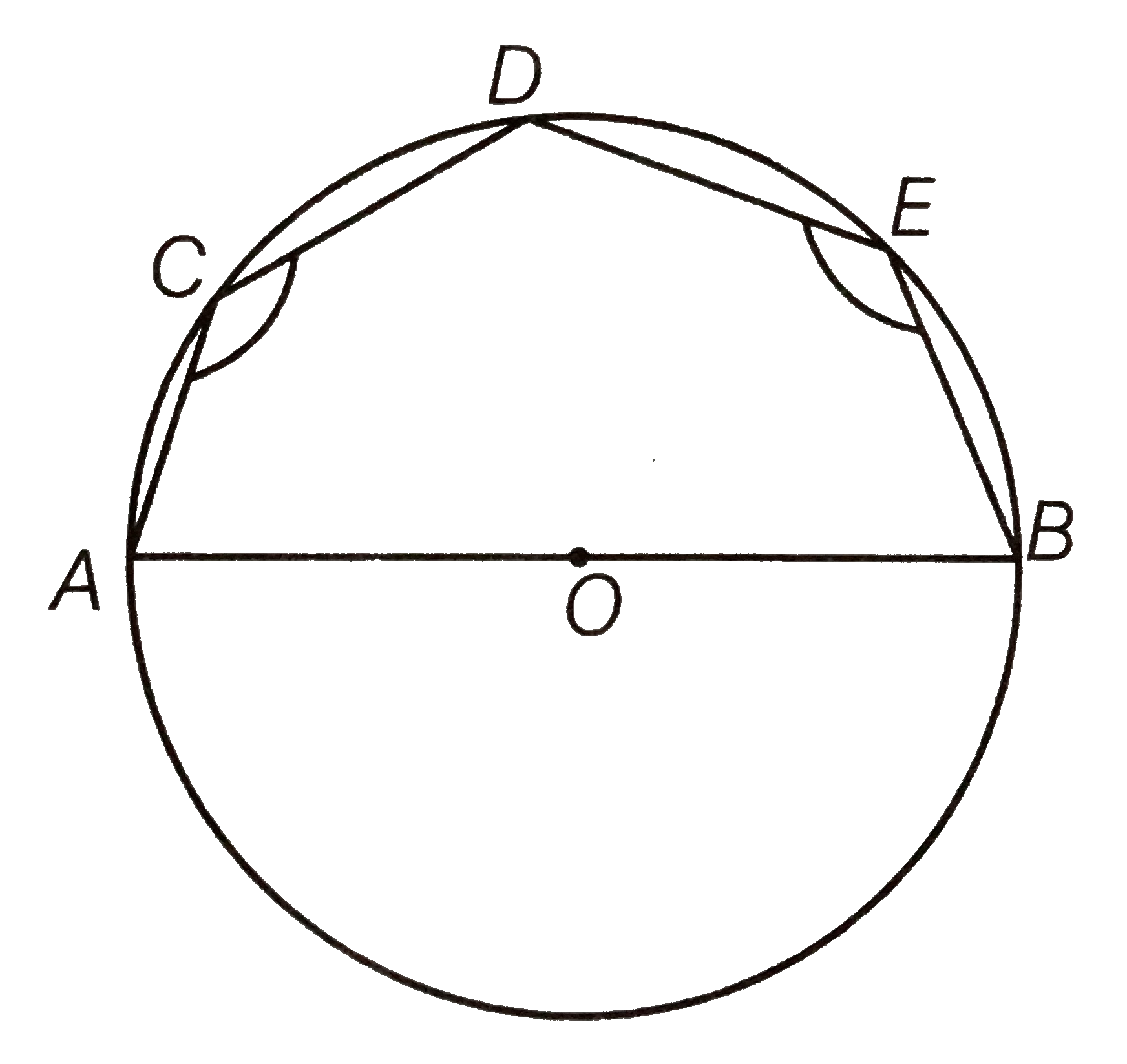
In the given figure, join AE.
Since, A, C, D and E are four point on a circle, then ACDE is a cyclic quadrilateral.
∴∠ACD+∠AED=180∘ …(i)
[sum of opposite angles in a cyclic quadrilateral is 180∘]
Now, ∠AEB=90∘...(ii)
We know that, diameter subtends a right angle to the circle.

On adding Eqs. (i) and (ii), we get
(∠ACD+∠AED)+∠AEB=180∘+90∘=270∘
⇒∠ACD+∠BED=270∘
Topper's Solved these Questions
- CIRCLESBook:NCERT EXEMPLAR ENGLISHChapter:CIRCLESExercise:Exercise 10.4
Explore 14 Videos
- CIRCLESBook:NCERT EXEMPLAR ENGLISHChapter:CIRCLESExercise:Exercise 10.2
Explore 10 Videos
- Areas of Parallelograms and TrianglesBook:NCERT EXEMPLAR ENGLISHChapter:Areas of Parallelograms and TrianglesExercise:Exercise-9.4 Long Answer Type Questions
Explore 10 Videos
- CONSTRUCTIONSBook:NCERT EXEMPLAR ENGLISHChapter:CONSTRUCTIONSExercise:Long Answer Type Questions
Explore 5 Videos
Similar Questions
Knowledge Check
In the figure, A, B, C are points on the circle. What is the value of x?
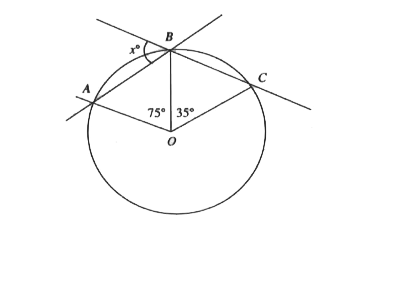 A45B55C60D65
A45B55C60D65In the figure, AB and CD are the diameters of the circle. What is the value of x?
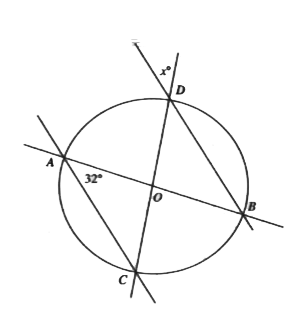 A16∘B18∘C26∘D32∘
A16∘B18∘C26∘D32∘
If AOB is a diameter of a circle and C is a point on the circle, then AC2+BC2=AB2.
View SolutionIn the adjoining figure, AB is the diameter of the circle and two points C and D are on the circle. If ∠CAD=45∘ and ∠ABC=65∘, then find the value of ∠DCA.
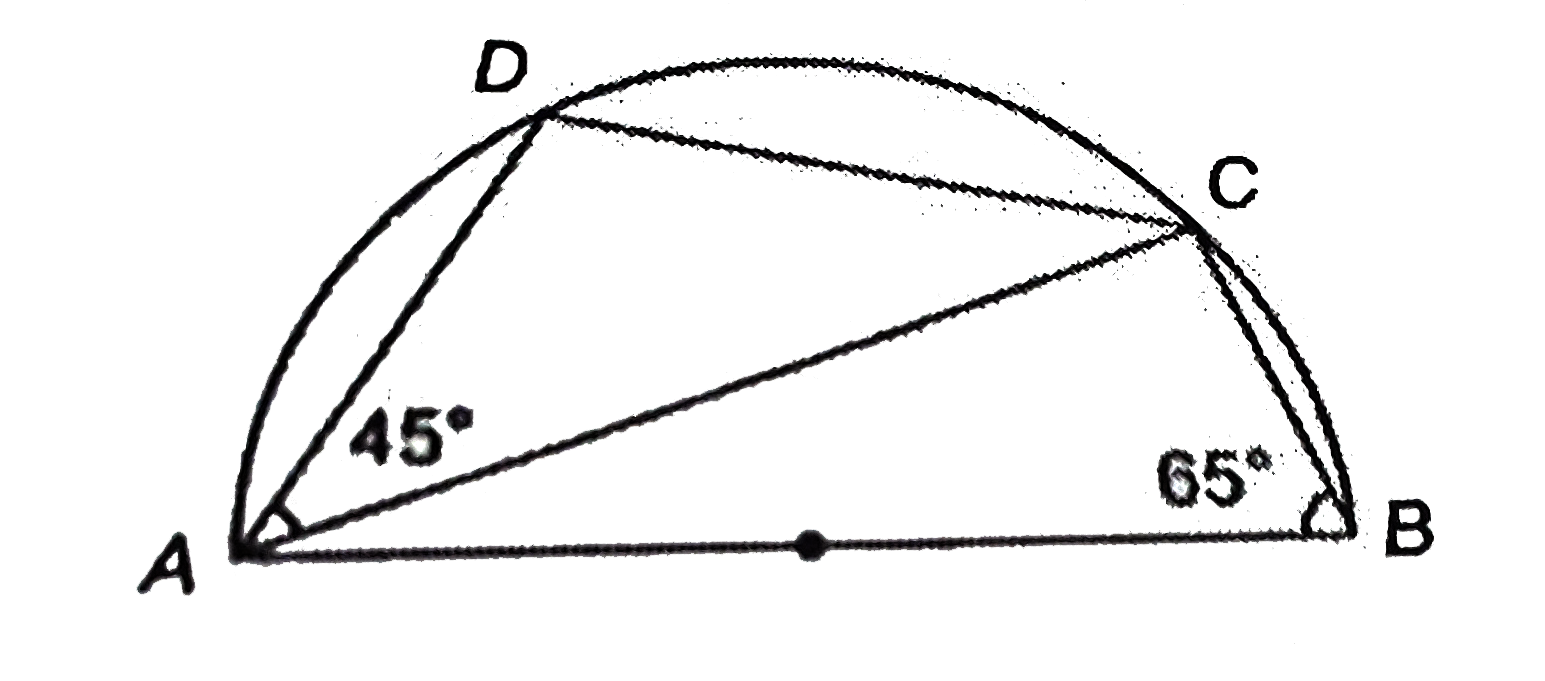
View SolutionAB is a diameter of a circle and C is any point on the circle. Show that the area of ABC is maximum, when it is isosceles.
View SolutionIn the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.

View SolutionIn Figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘
View SolutionIn the adjoining figure, AOB is the diameter and O is the centre of the circle. If ∠BDC=60∘, then find the value of ∠ABC.

View Solution