Calculate the solid angle subtended by the periphery of an area of 1cm2 at a point situated symmetrically at a distance of 5 cm from the area.
To calculate the solid angle subtended by the periphery of an area of 1cm2 at a point situated symmetrically at a distance of 5cm, we can use the formula for solid angle Ω:
Ω=Ar2
where:
- A is the area,
- r is the distance from the area to the point.
1. Identify the given values:
- Area A=1cm2
- Distance r=5cm
2. Convert the area to square meters (since the SI unit of area is m2):
A=1cm2=1×10−4m2
3. Convert the distance to meters (since the SI unit of distance is m):
r=5cm=0.05m
4. Substitute the values into the solid angle formula:
Ω=Ar2=1×10−4m2(0.05m)2
5. Calculate r2:
r2=(0.05m)2=0.0025m2
6. Now substitute r2 back into the formula:
Ω=1×10−4m20.0025m2
7. Perform the division:
Ω=1×10−42.5×10−3=0.04steradian
8. Express the answer in scientific notation:
Ω=4×10−2steradian
Final Answer:
The solid angle subtended by the periphery of the area at the point is:
Ω=4×10−2steradian
- A is the area,
- r is the distance from the area to the point.
- Area A=1cm2
- Distance r=5cm
A=1cm2=1×10−4m2
r=5cm=0.05m
Ω=Ar2=1×10−4m2(0.05m)2
r2=(0.05m)2=0.0025m2
Ω=1×10−4m20.0025m2
Ω=1×10−42.5×10−3=0.04steradian
Ω=4×10−2steradian
The solid angle subtended by the periphery of the area at the point is:
Ω=4×10−2steradian
Topper's Solved these Questions
- UNITS AND MEASUREMENTS Book:NCERT EXEMPLAR ENGLISHChapter:UNITS AND MEASUREMENTS Exercise:Long Answer Type Questions
Explore 9 Videos
- UNITS AND MEASUREMENTS Book:NCERT EXEMPLAR ENGLISHChapter:UNITS AND MEASUREMENTS Exercise:Very Short Answer Type Questions
Explore 6 Videos
- THERMODYNAMICS Book:NCERT EXEMPLAR ENGLISHChapter:THERMODYNAMICS Exercise:LONG ANSWER TYPE QUESTIONS
Explore 5 Videos
- WAVESBook:NCERT EXEMPLAR ENGLISHChapter:WAVESExercise:LONG ANSWER TYPE QUESTIONS
Explore 5 Videos
Similar Questions
Knowledge Check
The solid angle subtended by the periphery of an area 1cm2 at a point situtated symmetrically at a distance of 5 cm from the area is
A2×10−2 steradianB4×10−2 steradianC6×10−2 steradianD8×10−2 steradian
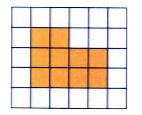
Calculate the area of the figure if each square is 1cm2
View SolutionSteradian is the solid angle subtended at the centre of the sphere by its surface whose area is equal to ____ of the sphere.
View SolutionA small air bubble is situated at a distance of 3 cm from the center of a glass sphere of radius 9 cm. When viewed from the nearest side, the bubble appears to be at a distance of 5 cm from the surface. Its apparent distance when viewed from the farthest side is n×5 cm where n is?
View SolutionCalculate the area of a rectangle whose length and breadth are 14.5 cm and 9.7 cm respectively.
View SolutionFind the area of a parallelogram with base 5 cm and altitude 4.2 cm.
View SolutionThe square on the diagonal of a cube has an area of 192cm2Calculate :
the total surface area of the cube.
View SolutionFind the area of a parallelogram with base 8 cm and altitude 4.5 cm.
View Solution
