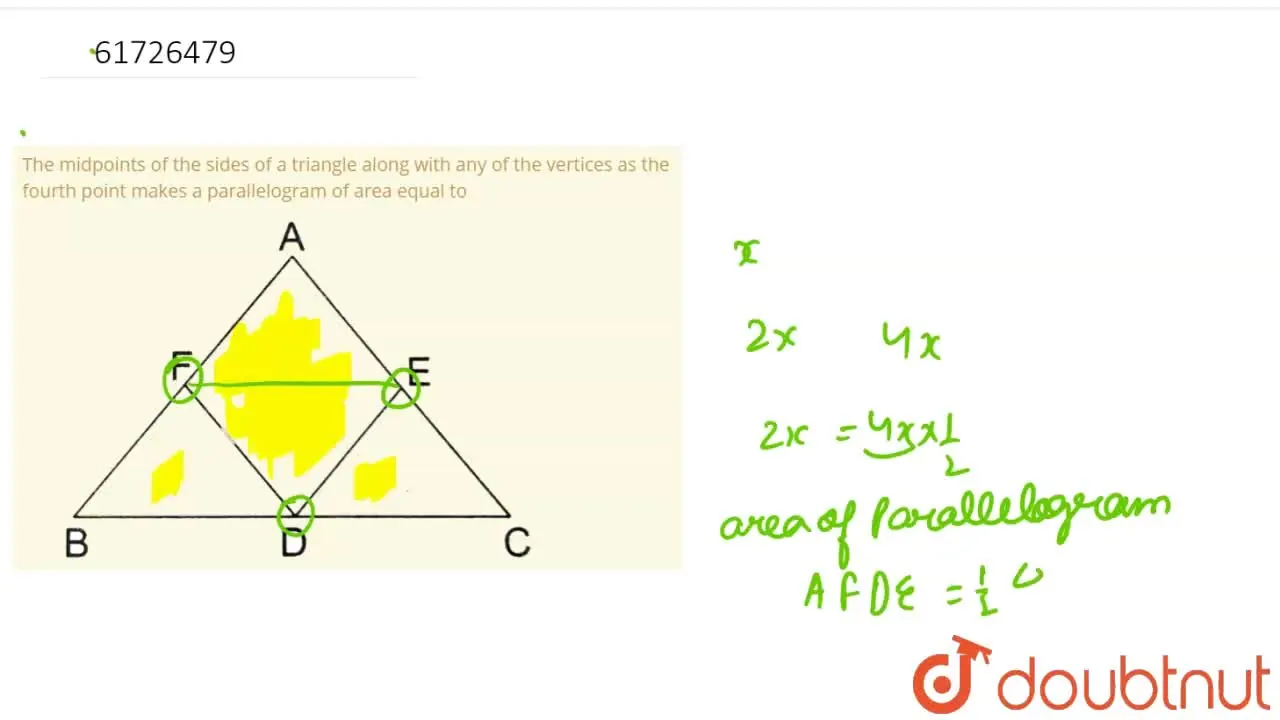
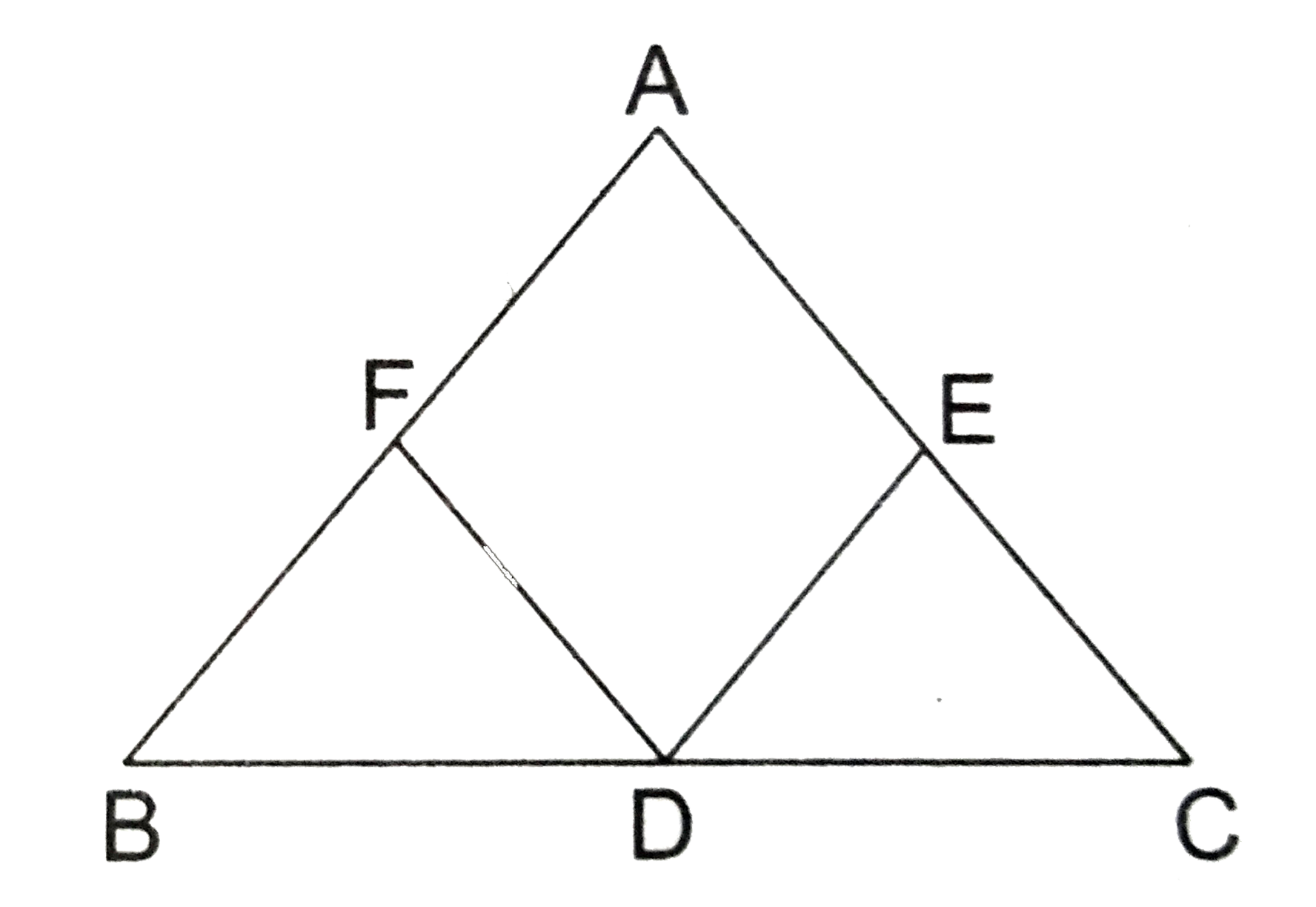
The midpoints of the sides of a triangle along with any of the vertices as the fourth point makes a parallelogram of area equal to
2(ar△ABC)
13(ar△ABC)
14(ar△ABC)
ar(△ABC)
The correct Answer is:A
Step by step video, text & image solution for The midpoints of the sides of a triangle along with any of the vertices as the fourth point makes a parallelogram of area equal to by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Related Playlists
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - Exercise 1138videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)16videos
AREAS OF TRIANGLES AND QUADRILATERALS
Similar Questions
The mid-point of the sides of triangle along with any of the vertices as the fourth point make a parallelogram of area equal to
View SolutionThe mid-point of the sides of triangle along with any of the vertices as the fourth point make a parallelogram of area equal to
View SolutionThe mid points of the sides of a triangle ABC along with any of the vertices as the fourth point make a parallelogram of area equal to:
(a)ar (ABC) (b) 12ar (ABC) 13ar (ABC) (d) 14 ar (ABC)View SolutionThe midpoints of the sides of a triangle are (3, 4) , (4, 1) and (2, 0) . Find the vertices of the triangle .
View SolutionThe midpoint of two opposite sides of a quadrilateral and the midpoint of the diagonals are the vertices of a parallelogram. Prove that using vectors.
View SolutionIf the sides of a triangle are 4,5 and 6 cm, then area of the triangle is equal to :
View SolutionIf the sides of a triangle are 4,5 and 6 cm, then area of the triangle is equal to :
View SolutionFind the area of the triangle formed by joining the mid–points of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
View SolutionFind the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0,−1),(2,1)and(0,3). Find the ratio of this area to the area of the given triangle.
View SolutionIn an equilateral triangle another equilateral triangle is drawn inside joining the mid-points of the sides of given equilateral triangle and the process is continued up to 7 times. What is the ratio of area of fourth triangle to that of seventh triangle ?
View Solution