The mid
points of the sides of a triangle ABC
along with
any of the vertices as the fourth point make a parallelogram of area equal
to:
(a)ar (ABC)
(b) 12ar (ABC)
13ar (ABC)
(d) 14 ar (ABC)
D, E and F are the midpoints of sides BC, AC and AB respectively.
On joining FE, we divide △ABC into 4 triangles of equal area.
Also, median of a triangle divides it into two triangles with equal area.
ar(AFDE)=ar(△AFE)+ar(△FED)
2ar(△AFE)=2×14ar(△ABC)
12ar(△ABC)
Hence, option(b) is correct.
Topper's Solved these Questions
Similar Questions
The mid points of the sides of a triangle ABC along with any of the vertices as the fourth point make a parallelogram of area equal to:
(a)ar (ABC) (b) 12ar (ABC) 13ar (ABC) (d) 14 ar (ABC)
View SolutionIf ABCD is a parallelogram, then prove that ar(△ABD)=ar(△BCD)=ar(△ABC)=ar(△ACD)=12ar(∣∣gmABCD)
View Solution
Knowledge Check
The area of the triangle with vertices at the points (a,b+c),(b,c+a),(c,a+b) is
A0Ba+b+cCab+bc+caDNone of theseThe area of the triangle with vertices at the point (a,b+c),(b,c+a),(c,a+b) is
A0Ba+b+cCab+bc+caDnone of these
In Figure, P is a point in the interior of a parallelogram ABCD. Show that ar(APB)+ar(PCD)=12ar (||gmABCD) ar (APD)+ar (PBC)=ar (APB)+ar(PCD)

View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of aΔABC.Show that (i) BDEF is a parallelogram. (ii) ar (DEF)=14ar (ABC)(iii) ar (BDEF)=12ar (ABC)
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
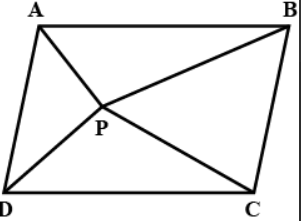
View SolutionAny point D is taken in the base BC of a triangle ABC and AD is produced to E, making DE equal to AD. Show that ar (BCE)=ar(ABC)
View SolutionIf D,E,F are the mid-points of the sides BC,CAandAB respectively of a triangle ABC, prove by vector method that AreaofDEF=14(areaofABC).
View SolutionABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove that: ar (ADO)=AR (CDO) ar ( ABP)= ar ( CBP)
View Solution

