A, B, C, D are mid-points of sides of a parallelogram PQRS. If ar (PQRS)=36cm2, then ar(ABCD)= 24 cm2 (b) 18 cm2 (c) 30 cm2 (d) 36 cm2
A, B, C and D are the midpoints of sides of a ∣∣gm PQRS.
area(△PQRS)=36cm2
The area of ||gm formed by joining AB, BC, CD and DA =12ar(∣∣gm PQRS)
=12×36
=18cm2
Hence, option (b) is correct.
Topper's Solved these Questions
Similar Questions
A, B, C, D are mid-points of sides of a parallelogram PQRS. If ar (PQRS)=36cm2, then ar(ABCD)= 24 cm2 (b) 18 cm2 (c) 30 cm2 (d) 36 cm2
View SolutionMedians of ABC intersect at G . If ar (ABC)=27 cm2, then ar (ABGC)= 6 cm2 (b) 9 cm2 (c) 12 cm2 (d) 18cm2
View SolutionIn a ABC, D, E, F are the mi-points of sides BC, CA and AB respectively. If ar(ABC)=16cm2, then ar (trapezium FBCE)= 4 cm2 (b) 8 cm2 (c) 12cm2 (d) 10cm2
View SolutionIn Figure, ABCDandFECG are parallelograms equal in area. If ar(AQE)=12cm2, then ar(IIgm)FGBQ)=
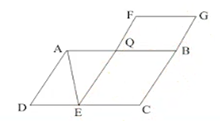
(a)12cm2
(b) 20cm2
(c) 24cm2
(d) 36cm2
View SolutionABCD is a parallelogram. P is any point on CD. If ar (DPA)=15 cm2 and ar (APC)=20cm2, then ar (APB)=
(a) 15cm2 (b) 20cm2 (c) 35 cm2 (d) 30cm2
View SolutionIn a ABC if D and E are mid-points of BC and AD respectively such that ar (AEC)=4 cm2 , then ar (BEC)= 4 cm2 (b) 6 cm2 (c) 8 cm2 (d) 12cm2
View SolutionABCDEF . If BC=3cm , EF=4cm and ar(ABC)=54cm2 , then ar(DEF)= 108cm2 (b) 96cm2 (c) 48cm2 (d) 100cm2
View SolutionP is the mid-point of side BC of a parallelogram ABCD such that ∠BAP=∠DAP. If AD=10cm, then CD= 5cm (b) 6cm (c) 8cm (d) 10cm
View SolutionABCD is a rectangle with O as any point in its interior. If ar (AOD)=3 cm2and ar (BOC)=6 cm2, then area of rectangle ABCD is: 9cm2 (b) 12 cm2 (c) 15cm2 (d) 18 cm2,
View SolutionThe area of the figure formed by joining the mid-points of the adjacent sides of a rhombus with diagonals 16cm and 12cm is 28 cm2 (b) 48 cm2 (c) 96 cm2 (d) 24 cm2
View Solution

