The given figure shows a pentagon ABCDE.EG drawn parallel to DA meets BA produced at G and CF drawn parallel to DB meets AB produced at F. Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.

ar(△DBC)=ar(△DBF)
ar(△ADE)=ar(△DBF)
ar(△DBC)+ar(△ADE)+ar(△ABD)=ar(△DBF)+ar(△ADG)+ar(△ABD)
∴ar(pentagonABCDE)=ar(△DGF).
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
32 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE
5 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE
5 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
The given figure shows a pentagon ABCDE .drawn parallel to DA meets BA produced at G and CF drawn parallel to DB meets AB produced at F. Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.
View SolutionIn figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar(ABCDE)=ar(ΔAPQ).
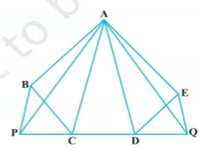
View SolutionIn Figure, ABCD is a quadrilateral and BE∣AC and also BE meets DC produced at E. Show that area of ADE is equal to the area of the quadrilateral ABCD
View SolutionIn Fig. 9.22, ABCD is a quadrilateral and BE ∣∣ ACand also BE meets DC produced at E. Show that area of ΔADEis equal to the area of the quadrilateral ABCD.
View SolutionIn Figure, ABCD is a quadrilateral and BE⊥AC and also BE meets DC produced at E , Show that area of ADE is equal to the area of the quadrilateral ABCD.
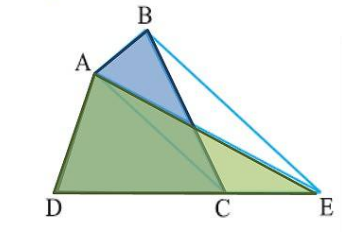
View SolutionThe side AB of a parallelogram ABCD is produced to any point E. A line through A and parallel to CE meets CB produced at G and then parallelogram EBGF is completed (see the figure). Prove that
area of ||gmABCD= area of ||gmBEFG.
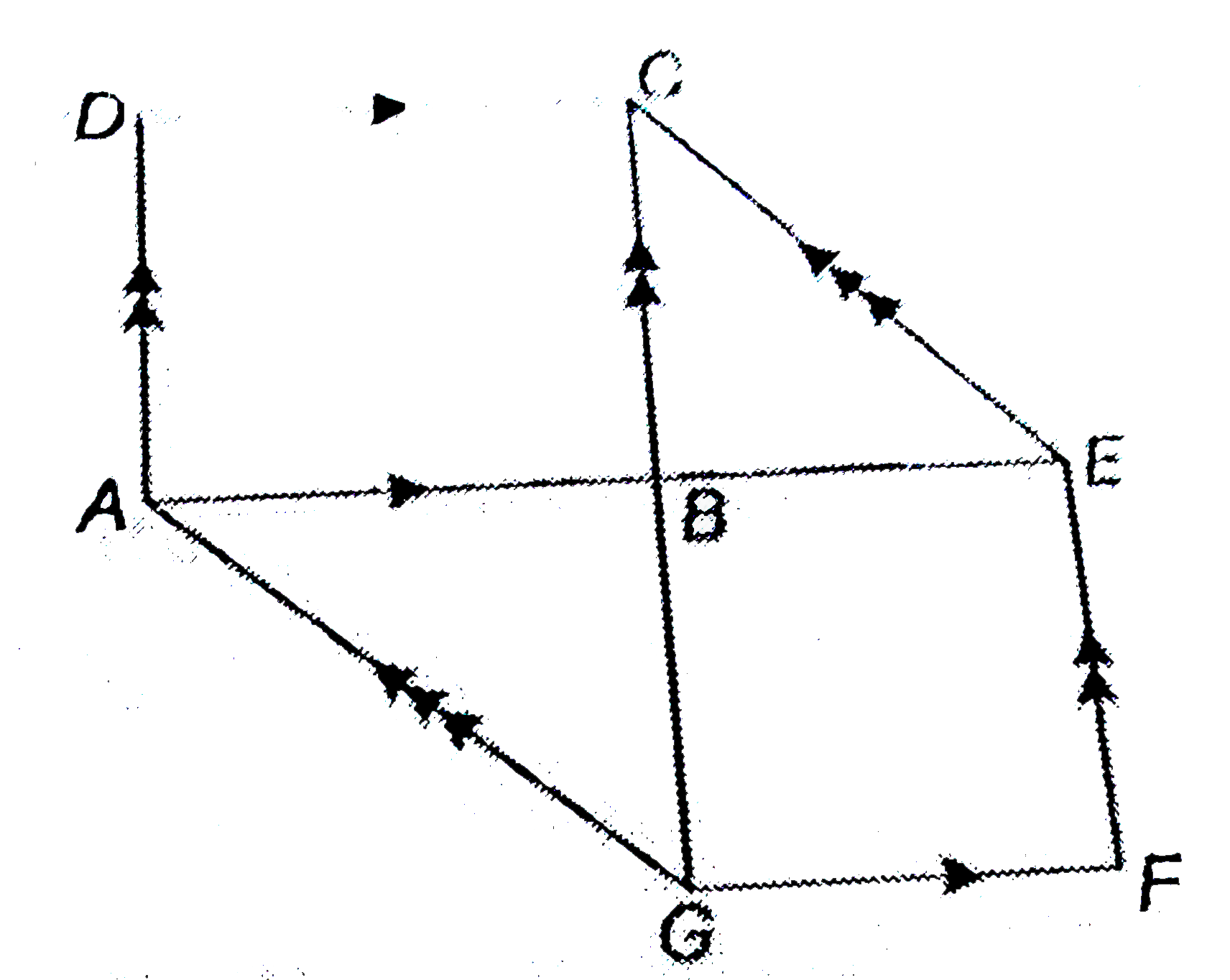
View SolutionIn the figure, ABCD is a quadrilateral. A line DP drawn parallel to diagonal AC from point D, meet BC produced at P. Prove that:
area of ΔABP= area of □ABCD
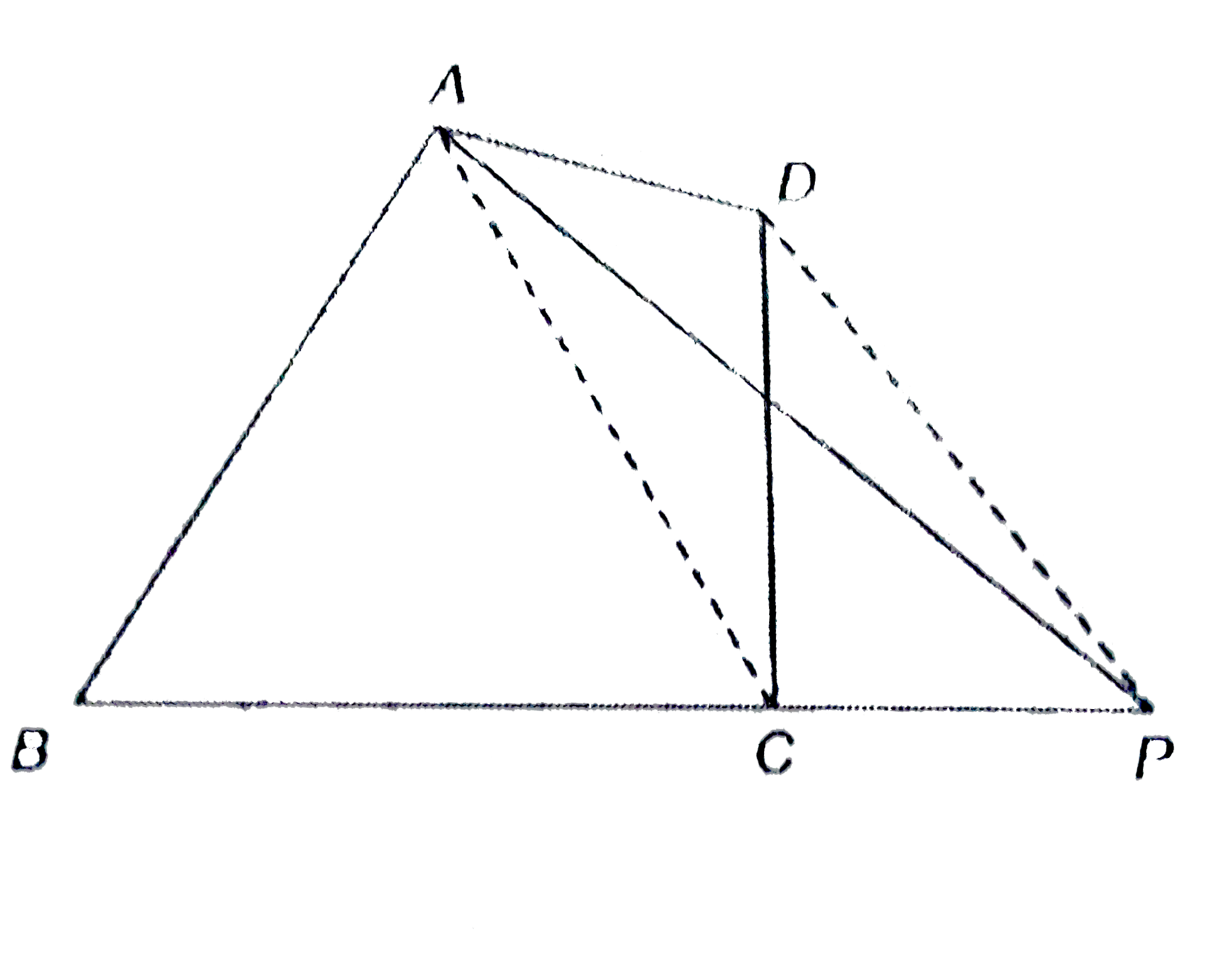
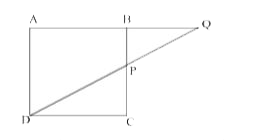
View SolutionIn the given figure, ABCD is a parallelogram. Point P is at BC such that PB : PC = 1 : 2. The extended DP and extended AB meets at point Q. If the area of BPQ is 20 unit2 then find the area of ΔDCP.
View SolutionIn the given figure, AP is parallel to BC, BP is parallel to CQ. Prove that the areas of triangle ABC and BQP are equal

View SolutionThe given figure shows a quadrilateral ABCD. Prove that :
AB+BC+CD+DA>AC+BD
View Solution
