O is the any point on diagonal PR of parallelogram PQRS. Prove that Ar(PSO) = Ar(PQO)
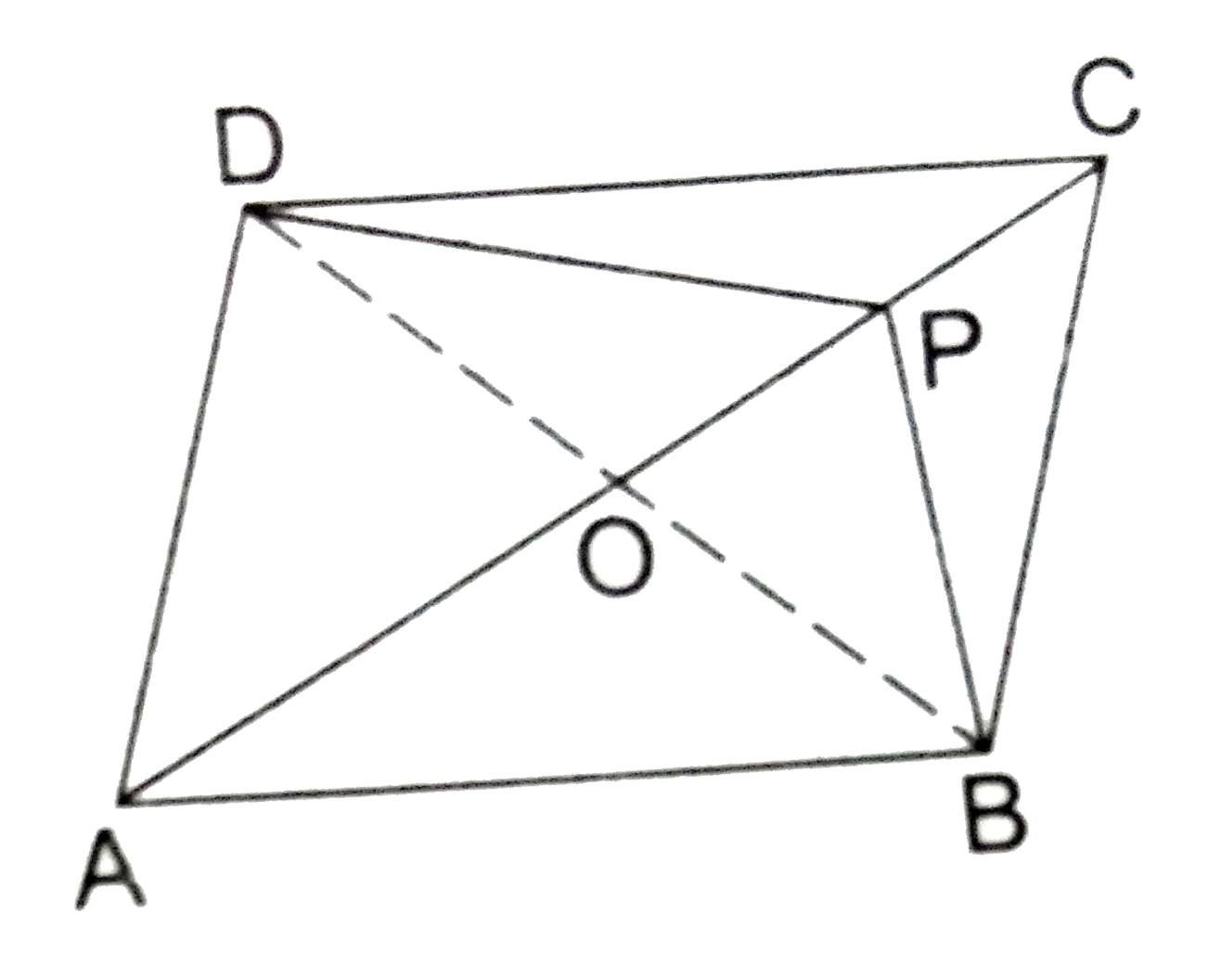
Draw diagonal BD. Let AC and BD intersect at O. Then, O is the midpoint of BD.
ar(△DPO)=ar(△BPO) [∴ PO is a median of △BPD].
ar(△ADO)=ar(△ABO) [∴ AO is a median of △ABD].
∴ar(△DPO)+ar(△ADO)=ar(△BPO)+ar(△ABO)
⇒ar(△ADP)=ar(△ABP).
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
32 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE
5 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE
5 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
Knowledge Check
Diagonals of a parallelogram PQRS must be a
ArectangleBsquareCcyclic quadrilateralDrhombus
O is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(OAB)=ar(OBC)
View SolutionP is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(△APD) = ar(△CPD).
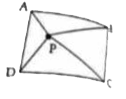
View SolutionIn the adjacent figure P is a point inside the parallelogram ABCD. Prove that
ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
View SolutionIn the adjacent figure P is a point inside the parallelogram ABCD. Prove that
ar (APB) + ar (PCD) = 12 ar (ABCD)
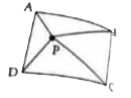
View SolutionIn the adjoining figure, P is the point in the interior of a parallelogram ABCD.Show that ar(DeltaAPB) ar(DeltaPCD) =1/2ar(||gm ABCD)
View SolutionIn Fig. 9.16, P is a point in the interior of a parallelogram ABCD. Show that(i) ar(APB)+ar(PCD)=12ar(ABCD)(ii) ar(APD)+ar(PBC)=ar(APB)+ar(PCD)
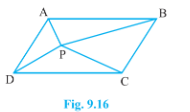
View SolutionIn the figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(△APB)+ar(△PCD=12ar(ABCD)
(ii) ar(△APD)+ar(△PBC)=ar(△APB)+ar(△PCD)

View Solution

