In Fig. 9.24, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that ar(△ABC)=ar(△ABD)
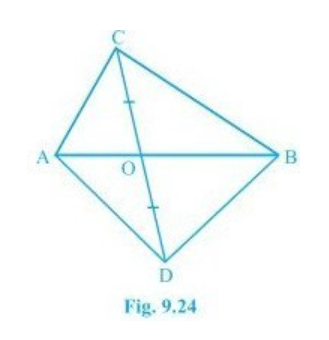
AO is the median of △CAD⇒ar(△COA)=ar(△DOA).
BO is the median of △CBD⇒ar(△COB)=ar(△DOB).
∴ar(△COA)+ar(△COB)=ar(△DOA)+ar(△DOB)⇒ar(△ABC)=ar(△ABD).
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES Book:RS AGGARWALChapter:AREAS OF PARALLELOGRAMS AND TRIANGLES Exercise:MULTIPLE-CHOICE QUESTIONS (MCQ)
Explore 32 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES Book:RS AGGARWALChapter:AREAS OF PARALLELOGRAMS AND TRIANGLES Exercise:ASSERTION & REASON TYPE
Explore 5 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES Book:RS AGGARWALChapter:AREAS OF PARALLELOGRAMS AND TRIANGLES Exercise:ASSERTION & REASON TYPE
Explore 5 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBook:RS AGGARWALChapter:AREAS OF TRIANGLES AND QUADRILATERALSExercise:Multiple Choice Questions (Mcq)
Explore 16 Videos
Similar Questions
In figure, ABC and ABD are two triangles on the same base AB. If line segment CD is bisected by AB at O , show that ar(△ABC)=ar(△ABD).
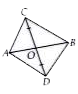
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).

View SolutionIn Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)= AODO
View Solution△ABCand△DBC are two triangles on the same base BC. A and D lies on opposite sides of BC. Prove that ar(△ABC)ar(△DBC)=AODO
View SolutionIn the adjoining figure, △ABCand△DBC are on the same base BC with A and D on opposite sides of BC such that ar(△ABC)=ar(△DBC). Show that BC bisect AD.
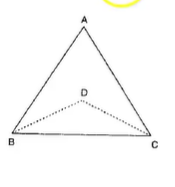
View SolutionIn the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
(i)ar(△BDE)=14ar(△ABC)
(ii)ar(△BDE)=12ar(△BAE)
(iii)ar(△ABC)=2ar(△BEC)
(iv)ar(△BFE)=ar(△AFD)
(v)ar(△BFE)=2ar(△FED)
(vi)ar(△FED)=18ar(△AFC).

View SolutionIn Figure, ABC and DBC are two triangles on the same base BC such that AB=AC and DB=DC. Prove that ∠ABD=∠ACD
View SolutionIn Figure, ABC and DBC are two isosceles triangles on the same base BC such that AB=AC and DB=CD. Prove that ∠ABD= ∠ACD
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
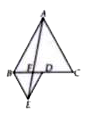
ar(ΔABC) = 2 ar(ΔBEC)
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar(△BED)=14ar(△ABC).
View Solution