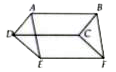
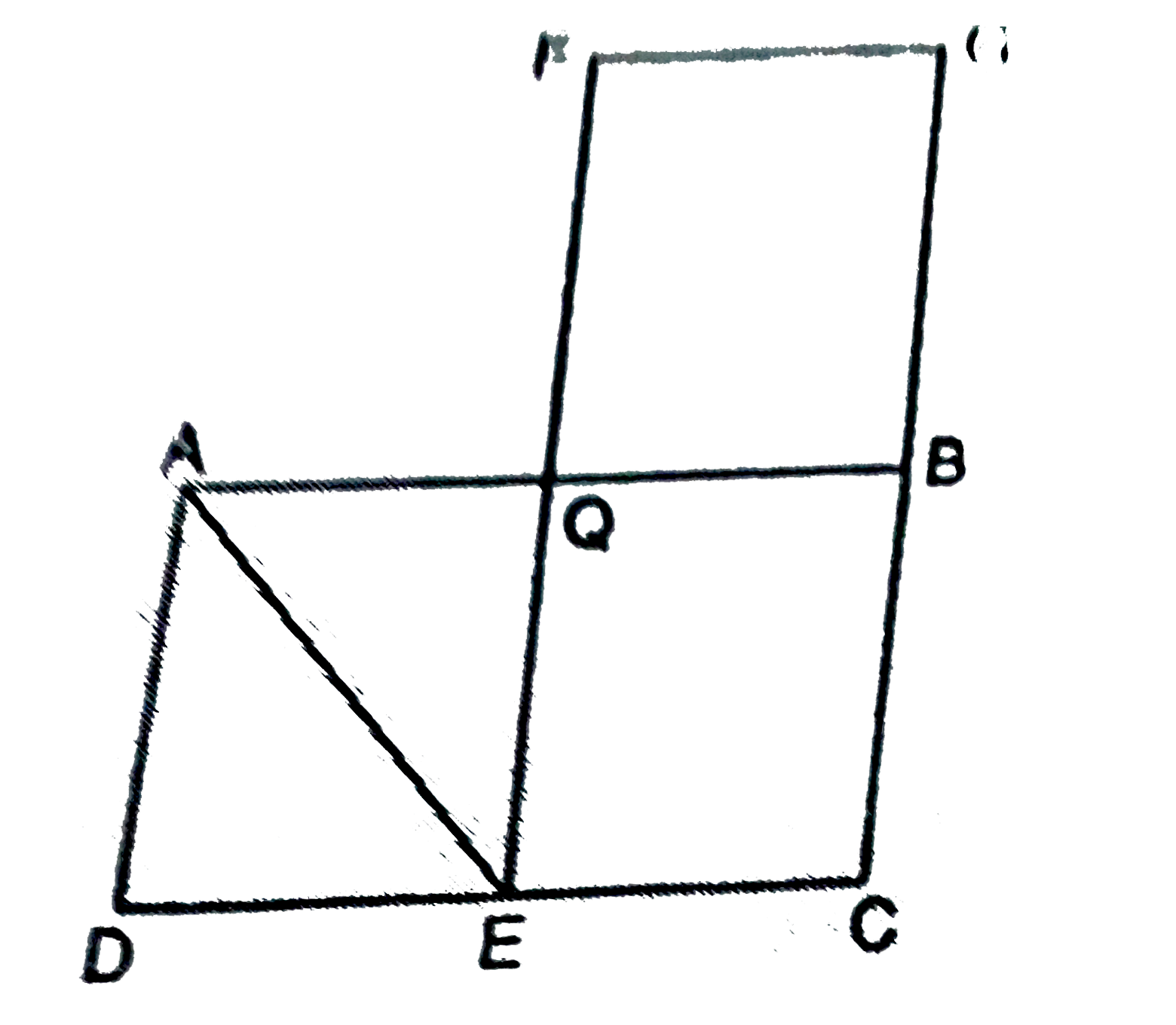
In figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
Video Solution
Text Solution
△CPD and ||gm ABCD are on the same base DC and between the same prallels CD and AB.
∴ar(△CPD)=12ar(||gm ABCD).
Similarly, ar(△AQD)=12ar(||gm ABCD).
∴ar(△CPD)=ar(△AQD).
|
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - Exercise 11
38 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
32 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
Knowledge Check
In the given figure, ABCD and AEFD a re two parallelograms.
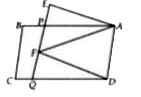
ar(ΔPEA) =Aar(∣∣gmΔPEA)Bar(ΔPFD)Car(ΔQFD)Dar(∣∣gmΔCQPB)In the given figure, ABCD and AEFD a re two parallelograms.

PE =ABPBFQCAPDCQIn the given figure, ABCD and AEFD a re two parallelograms.
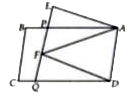
(ar(ΔAPE))/(ar(ΔPFA)) =A(ar(ΔQFD))/(ar(ΔPFD))B(ar(ΔAEF))/(ar(ΔPFD))C(ar(ΔQFD))/(ar(ΔAEF))DNone of these
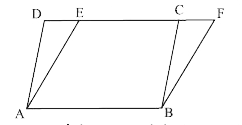
In Fig. 9.31, ABCD, DCFE and ABFE are parallelograms. Show that ar(ADE)=ar(BCF).
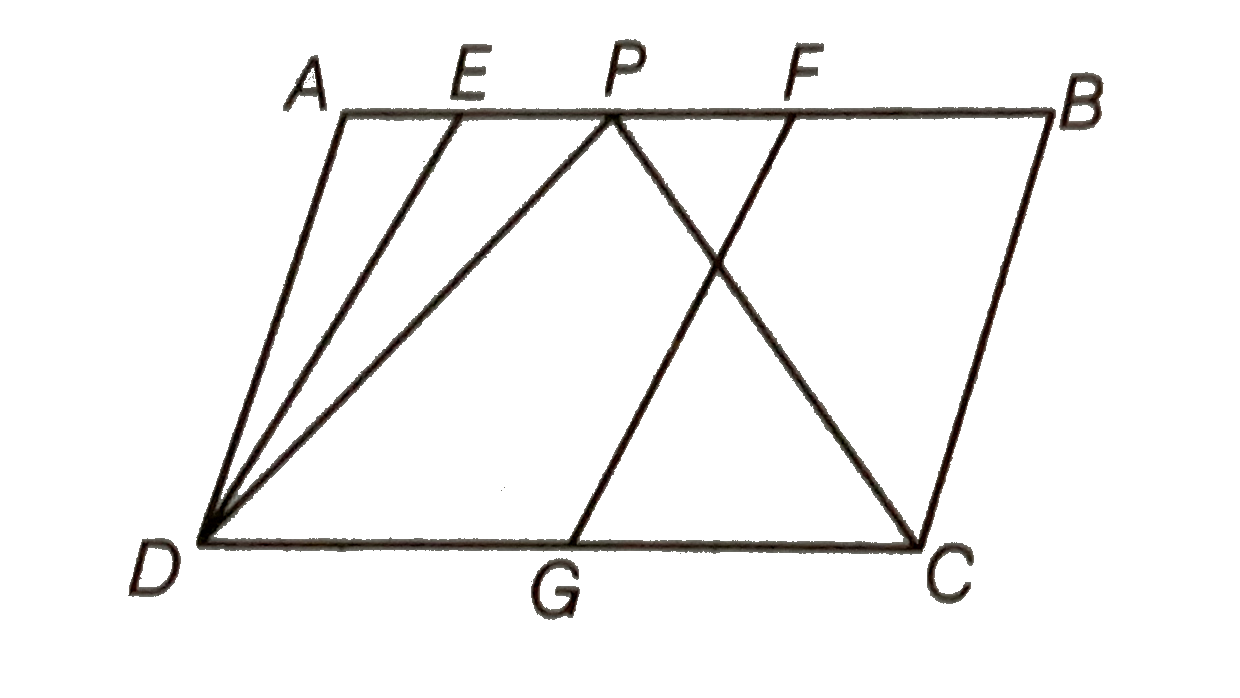
View SolutionIn the given figure, ABCD and FECG are parallelograms equal in area. If ar(ΔAQE)=12cm2, find ar(∣∣gmFGBQ)
View SolutionIn the figure ABCD and ABFE are Parallelograms then find ar (ΔBCF).
If ar (ABCE)=18cm2
ar (ABCD)=25cm2
View SolutionIn the figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then, ar(ΔDPC)=ar(EFGD).
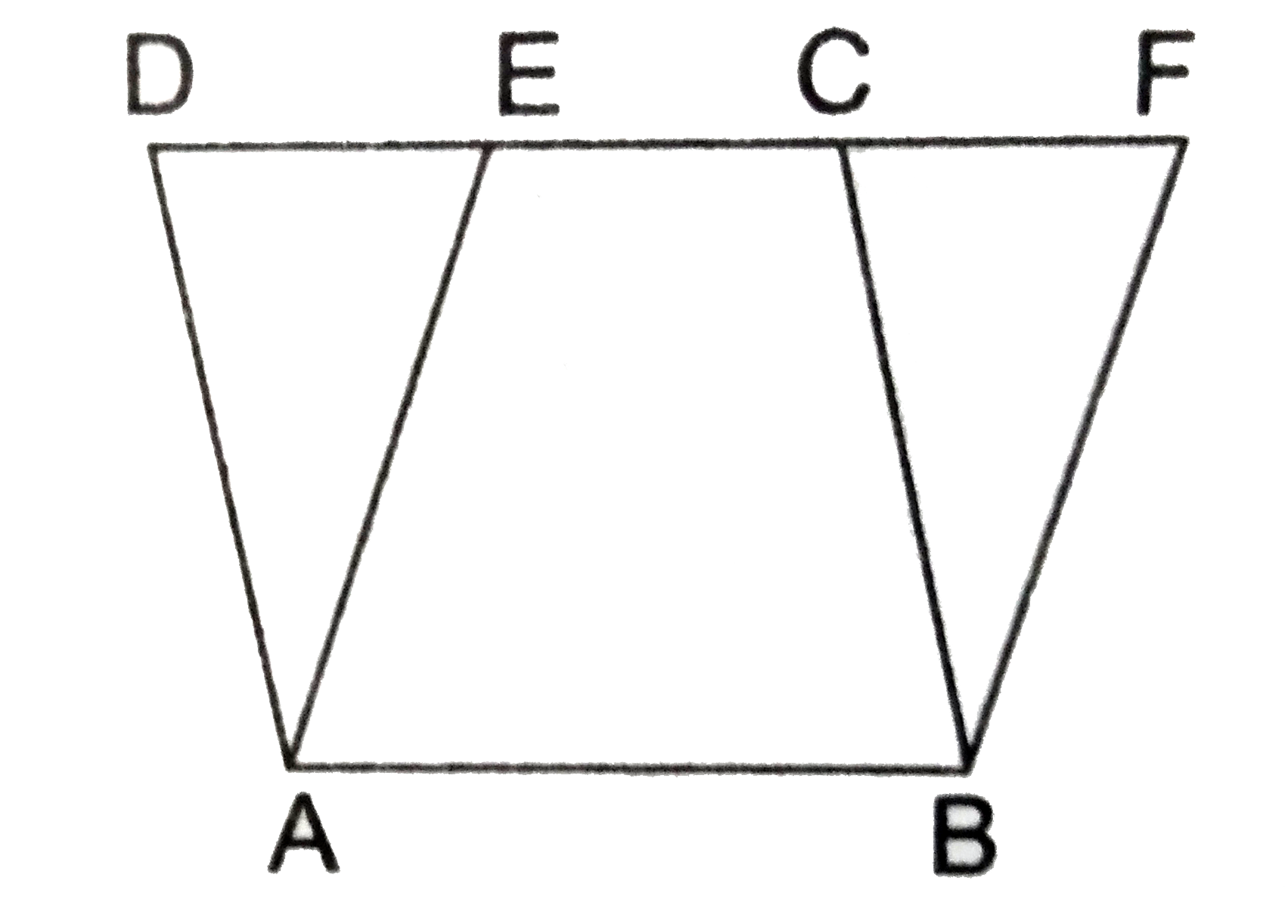
View SolutionIn the given figure, ABCD and ABEF are parallelograms such that ar(quad. EABC) 17cm2 and ar(||gm ABCD) =25cm2. Then ar(△BCF) = ?
View Solution