In the given figure, ΔABC is an isosceles triangle in which AB=AC and a circle passing through B and C intersects AB and AC at D and E respectively. Prove that DE∣∣BC
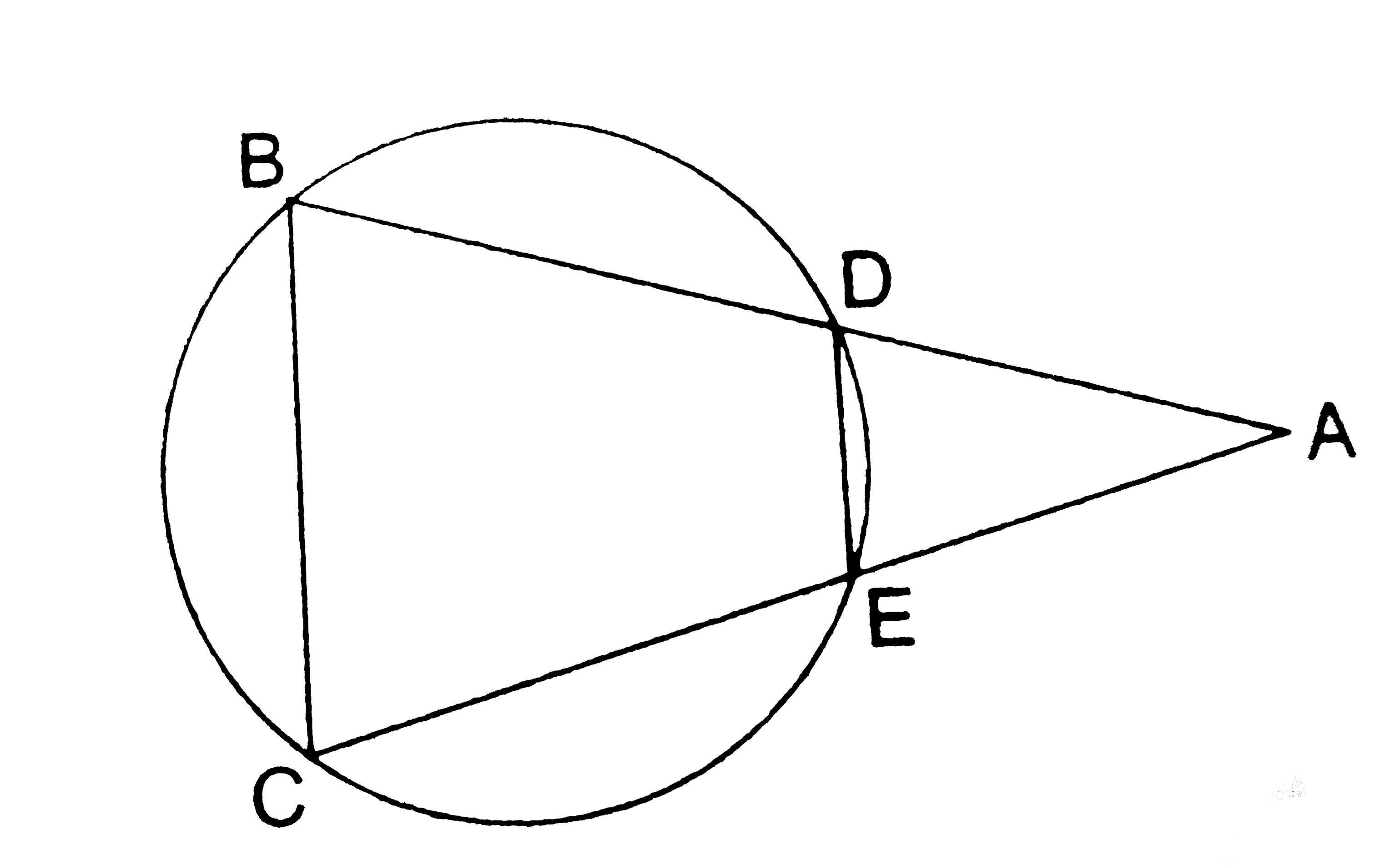
AB=AC⇒∠ACB=∠ABC.
∴ext. ∠ADE=∠ACB=∠ABC
Thus, ∠ADE=∠ABC⇒DE∣∣BC.
Topper's Solved these Questions
- CIRCLES Book:RS AGGARWALChapter:CIRCLES Exercise:Multiple Choice Questions (Mcq)
Explore 5 Videos
- CIRCLES Book:RS AGGARWALChapter:CIRCLES Exercise:MULTIPLE CHOICE QUESTION(MCQ)
Explore 37 Videos
- CIRCLES Book:RS AGGARWALChapter:CIRCLES Exercise:EXERCISE 12B
Explore 18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBook:RS AGGARWALChapter:BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONExercise:EXERCISE 17B
Explore 16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Multiple Choice Questions (Mcq)
Explore 20 Videos
Similar Questions
In an isosceles triangle ABC with AB=AC, a circle passing through B and C intersects the sides ABandAC atDandE respectively. Prove that DECB.
View SolutionIn an isosceles triangle ABC with AB=AC, a circle passing through B and C intersects the sides AB and AC at D and E respectively. Prove that DEBC
View Solution
Knowledge Check
In the adjoining figure, ABC is an isosceles triangle in which AB = AC. If E and F be the midpoints of AC and AB respectively, then
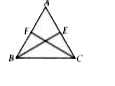 ABE = CFB∠BFC=∠CEBCBF = CEDAll of these
ABE = CFB∠BFC=∠CEBCBF = CEDAll of theseIn the adjoining figure, ABC is an isosceles triangle in which AB=AC. If E and F be the midpoints of AC and AB respectively, then
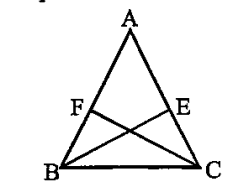 ABE=CFB∠BFC=∠CEBCBF=CEDAll of these
ABE=CFB∠BFC=∠CEBCBF=CEDAll of these
In the given figure, ΔABC is an isosceles triangle in which AB=AC and AE bisects ∠CAD. Prove that AE∣∣BC.
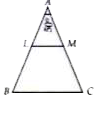
View SolutionIn the figure, ABC is an isosceles triangle in which AB = AC and LM is parallel to BC. If ∠A=50∘ find ∠LMC.
View SolutionThe incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively . Prove that BD = DC.

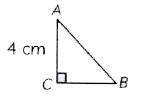
View SolutionIn the given figure, △ABC is an isosceles triangle right angled at C with AC = 4 cm. Find the length of AB.
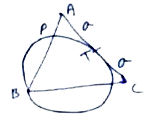
View SolutionABC is an isosceles Δ, AB = AC . A circle passing through B touch AC at mid point T and cut AB at P. find APAB ?
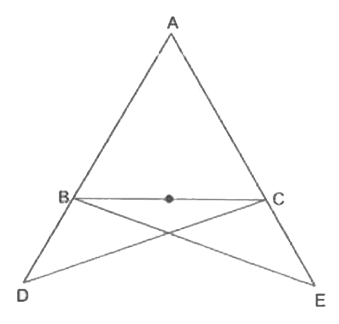
View SolutionIn the given figure, △ABC is an isosceles triangle in which AB - AC. If AB and AC are produced to D and E respectively such that BD = CE, prove that BE = CD. Hint. Show that △ACD=△ABE.
View Solution

