In the given figure, AB is a diameter of a circle with centre O and DO∣∣CB.
In ∠BCD=120∘, calculate
(i)∠BAD , (ii) ∠ABD
(iii) ∠CBD, (iv) ∠ADC
Also, show that ΔAOD is an equilateral triangle.
The correct Answer is:(i)∠BAD=60∘,(ii)∠ABD=30∘,(iii)∠CBD=30∘,(iv)∠ADC=120∘
∠BCD+∠BAD=180∘⇒BAD=60∘
∠BAD=90∘ [ angle in a semicircle ]
∠BDA+∠BAD+∠ABD=180∘⇒∠ABD=30∘
OD=OA⇒∠ODA=∠OAD=∠BAD=60∘
∴∠ODB=90∘−∠ODA=30∘
∴∠CBD=∠ODB=30∘⇒∠CDB=180∘−(120∘+30∘)=30∘
and ∠ADC=∠ADB+∠CDB=(90∘+30∘)=120∘
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Multiple Choice Questions (Mcq)
5 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12B
18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
In the given figure, AB is a diameter of the circle with centre O and DO||CB.If ∠BCD=120∘,calculate 1. ∠BAD 2. ∠ABD 3. ∠CBD 4. ∠ADC Also show that AOD is an equilateral triangle
View SolutionIn the given figure, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ=58∘, find ∠ATQ.
View Solution
Knowledge Check
In the given figure, BOD is the diameter of the circle with centre O. ∠COD=92∘and∠ABD=65∘. Then y equals
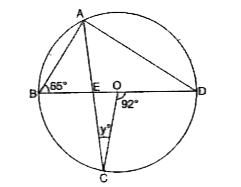 A65∘B46∘C44∘D21∘
A65∘B46∘C44∘D21∘AB is a diameter of the circle with centre O, CD is chord of the circle. If ∠BOC=120∘, then the value of ∠ADC is
A42∘B30∘C60∘D35∘
In the given figure, AB is diameter of a circle with centre O and AT is a tangent at ∠AOQ=58∘, find ∠ATQ.
View SolutionIn the giben figure, AB is the diameter of the circle, with centre O and AT is the tangent. Calculate the calue of x.
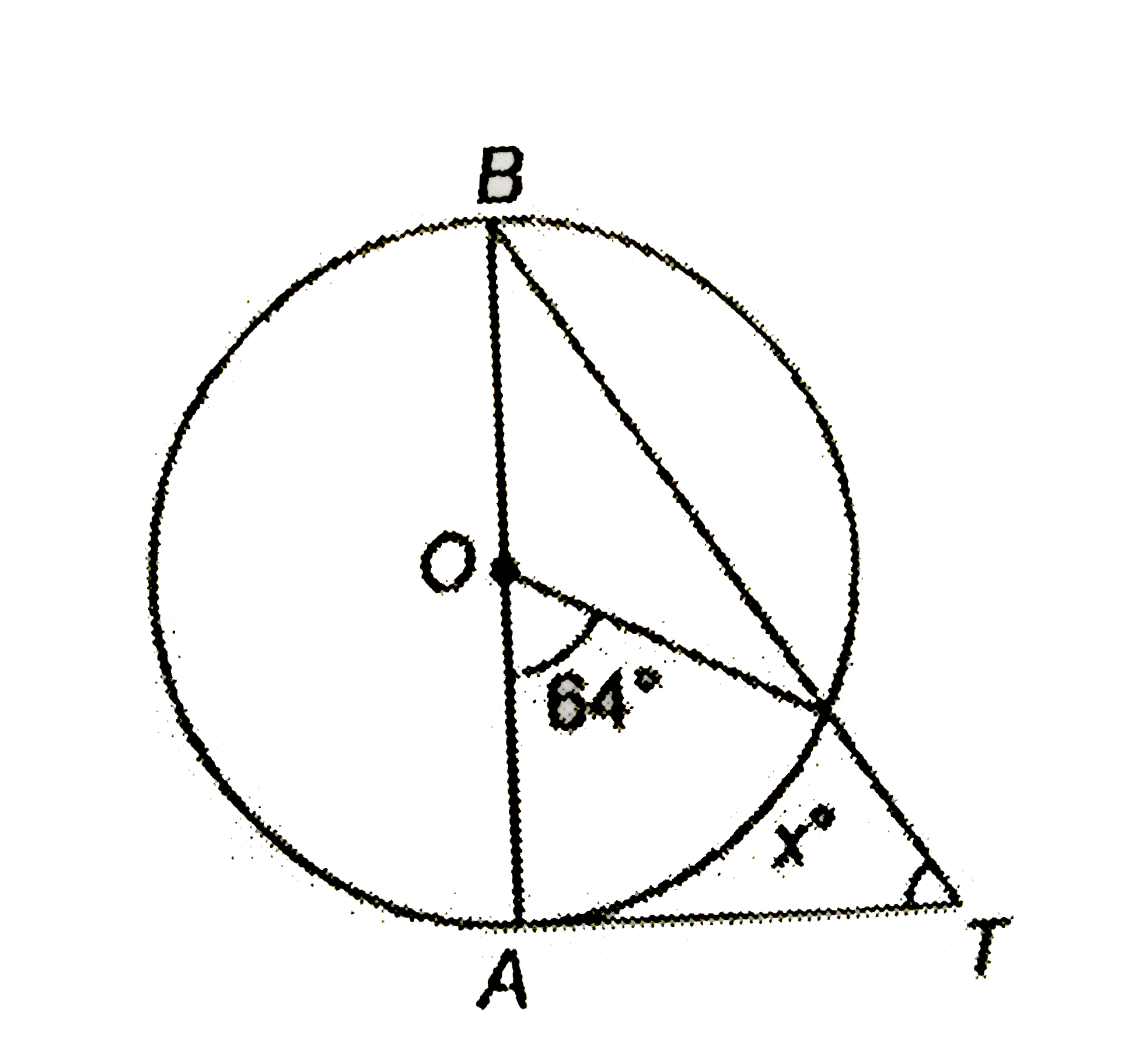
View SolutionIn the figure given below, AD is a diameter of a circle with centre O.If AB ll CD, prove that AB=CD
View SolutionIn the given figure, AB is the diameter of the circle. ∠ADC=120∘. Find ∠CAB :
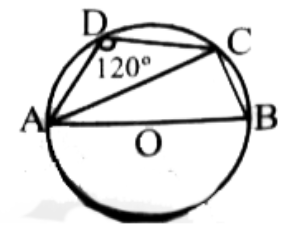
View SolutionIn the given fig. OP is equal to the diameter of the circle with centre O. Prove that ΔABP is an equilateral triangle.
View SolutionIn the figure, ABC is a triangle inscribed in a circle with centre O.
If AB = AC = 15 cm and BC = 5 cm, calculate the radius of the circle.
View Solution
