Give a geometrical construction for finding the fourth point lyingon a circle passing through three given points, without finding the centre of the circle. Justify the construction.
Video Solution
Text Solution
Let A,B,C be the given points. With B as centre and radius equal to AC draw an arc. With C as centre and AB as radius draw another arc, intersecting the previous arc at D. Then, D is the desired point.
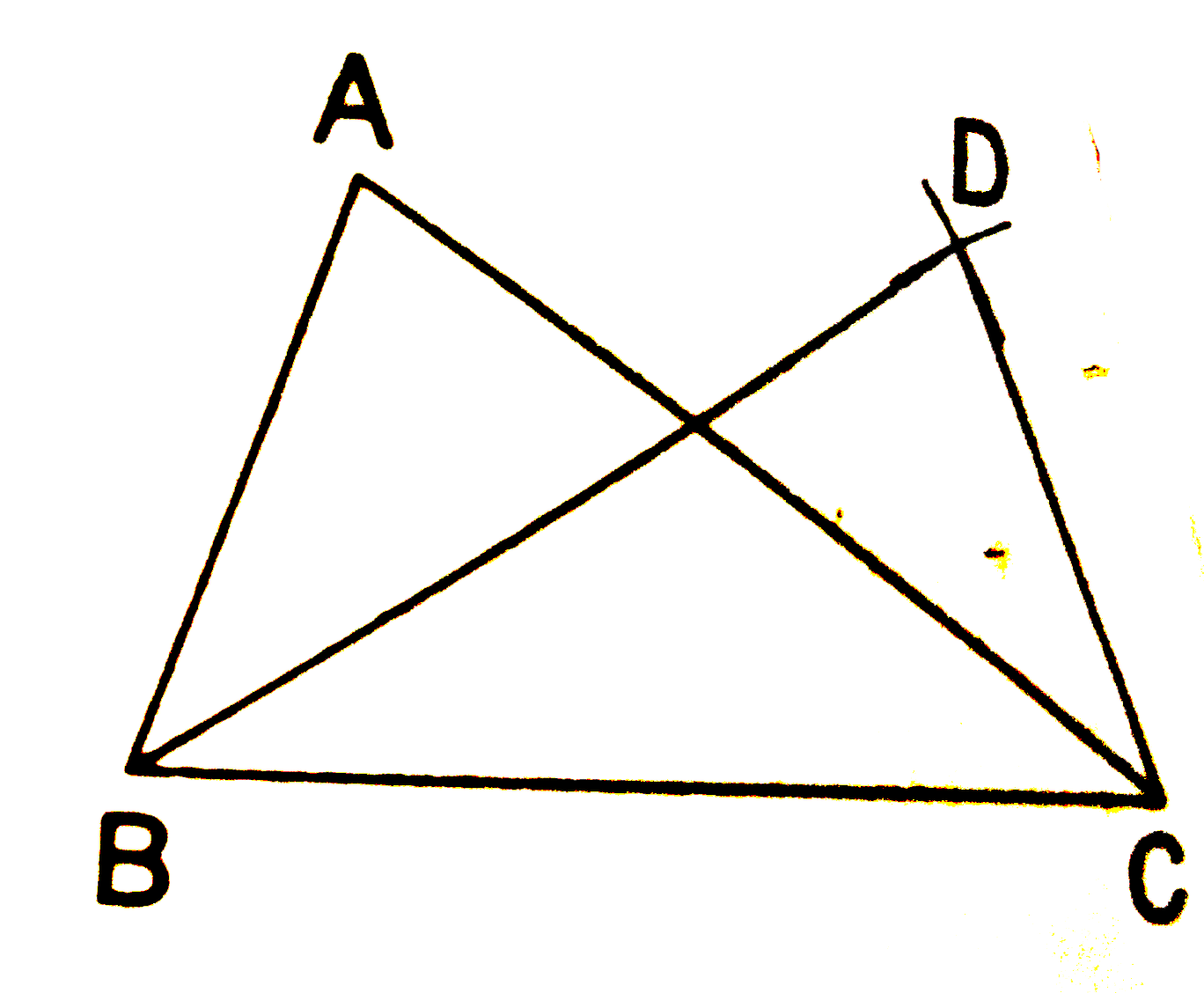
PROOF Join BD and CD.
ΔABC≅ΔDCB[∵AB=DC,AC=DB and BC=CB]
⇒∠BAC=∠CDB
Thus, BC subtends equal angles ∠BAC and ∠CDB on the same side of it.
∴point A,B,C,D are cyclic.
|
Similar Questions
Knowledge Check
How many circles can pass through three collinear points?
AoneBtwoCzeroDinfinitely manyHow many circles can pass through three non-collinear points?
AoneBtwoCzeroDinfinitely manyIf a circle passes through the points (0,0),(a,0) and (0,b), then find the coordinates of its centre.
A(a2,b2)B(−a2,−b2)C(a,b)Dnone of these
Find the centre of a circle passing through the points (6,−6), (3,−7) and (3,3).
View SolutionDraw any circle. Take any point on it and construct tangent at A without using the centre of the circle.
View SolutionFind the equation of a circle passing through the points (5,7),(6,6)and(2,−2). Find its centre and radius.
View SolutionFind the equation of a circle passes through the point (1,-1) and whose centre is at origin.
View SolutionConsider a circle passing through the origin and the points (a,b) and (−b,−a). On which line does the centre of the circle lie? What is the sum of the squares of the intercepts cut-off by the circle on the axes?
View Solution
